Главная Прочие дисциплины Книги Математичне програмування - Наконечний С.І.

Математичне програмування - Наконечний С.І.

11.5. Геометрична інтерпретація гри 2 x 2

Найпростішим випадком скінченної гри є парна гра, коли у кожного учасника є дві стратегії.

Розглянемо випадок, коли гра не має сідлової точки. Отже, . Необхідно знайти змішані стратегії та ціну гри. Позначимо шукані значення ймовірноcтей застосування «чистих» стратегій гравця А через , а для гравця В — через .

Згідно з основною теоремою теорії ігор, якщо гравець А притримується своєї оптимальної стратегії, то виграш буде дорівнювати ціні гри. Отже, якщо гравець А притримуватиметься своєї оптимальної стратегії , то:

(11.3)

Оскільки , то . Підставивши цей вираз у систему рівнянь (11.3), отримаємо:

.

Розв’язавши дане рівняння відносно невідомого , маємо:

, (11.4)

тоді: =. (11.5)

Провівши аналогічні міркування стосовно гравця В, маємо:

(11.6)

Оскільки , то .

.

Розв’язавши це рівняння відносно невідомого , маємо:

, (11.7)

тоді: . (11.8)

Ціну гри u знаходять, підставлючи значення (або ) в будь-яке з рівнянь (11.3) або (11.6):

. (11.9)

Знайти розв’язок гри з платіжною матрицею:

Розв’язання. Переконаємося, що гра не має сідлової точки:

,

.

Отже, ця гра не має сідлової точки. Скористаємося формулами (11.4), (11.5), (11.7), (11.8), (11.9). Маємо:

;

;

;

.

Ціна гри .

Отже, оптимальна стратегія кожного гравця полягає в тому, щоб випадково чергувати свої «чисті» стратегії. Гравець А має використовувати першу стратегію з імовірністю , а другу — з імовірністю , а гравець В — навпаки. За цих умов середній виграш дорівнюватиме 3,5.

Розв’язку гри 2 x 2 можна дати наочну геометричну інтерпретацію.

Розглянемо гру з платіжною матрицею виду:

Відмітимо на осі абсцис відрізок довжиною, що дорівнює одиниці (рис. 11.1). Лівий кінець відрізка (точка з абсцисою х = 0) буде відповідати стратегії А1, а правий кінець (х = 1) — стратегії А2, всі проміжні точки цього відрізка відповідатимуть змішаним стратегіям гравця А, причому імовірність х1 стратегії А1 буде дорівнювати відстані від точки Р до правого кінця відрізка, а ймовірність х2 стратегії А2 — відстані до лівого кінця відрізка. Проведемо через точки А1 та А2 два перпендикуляри до осі абсцис: вісь І і вісь ІІ. На першій з них відмітимо виграш за вибору стратегії А1, а на другій — за стратегії А2.

Нехай противник вибрав стратегію В1, їй відповідають на осях І та ІІ дві точки В1, причому довжина відрізка А1В1 дорівнює а11, а довжина відрізка А2В1 дорівнює а12.

Аналогічно будуємо пряму В2В2, яка відповідає стратегії В2.

Необхідно знайти оптимальну стратегію Х*, таку, за якої мінімальний виграш гравця А буде максимальним. Для цього виділимо жирною лінією на малюнку нижню межу виграшу за умови вибору стратегій В1 та В2, тобто ламану лінію В1МВ2. На цій межі знаходяться значення мінімального виграшу гравця А за будь-якої його змішаної стратегії. Очевидно, що найкраще з можливих мінімальних значень у нашому прикладі знаходиться в точці М, а в загальному випадку відповідає тій точці, де крива, що позначає мінімальний виграш гравця А, набуває максимального значення. Ордината цієї точки є ціною гри u. Відстань до лівого кінця відрізка х2 та відстань до правого кінця відрізка — х1 дорівнюють відповідно ймовірностям стратегій А2 та А1.

Рис. 11.1

Геометрична інтерпретація дає також змогу наочно зобразити нижню та верхню ціну гри (рис. 11.2). Для нашого прикладу нижньою ціною гри є величина відрізка А2В2, а верхньою ціною гри — А2В1.

Рис. 11.2

На цьому ж рисунку можна розглянути і геометричну інтерпретацію оптимальних стратегій противника В. Дійсно, частка стратегії В1 в оптимальній змішаній стратегії дорівнює відношенню довжини відрізка КВ2 до суми довжин відрізків КВ2 та КВ1 на осі І: .

З наведених міркувань легко висновувати, що гру 2 x 2 можна розв’язати елементарними прийомами. Аналогічно може бути розв’язана гра 2 x n, тобто коли гравець А має лише дві стратегії, а гравець В – n. У такому разі на рисунку слід зобразити перетин n прямих, що відповідатимуть n стратегіям гравця В. Мінімальні виграші гравця А являтимуть собою також ламану лінію, максимальне значення якої і визначатиме оптимальну стратегію для гравця А (рис. 11.3).

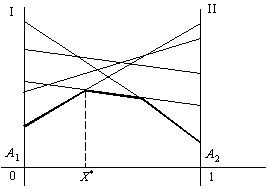
Рис. 11.3

Можна також розв’язати і гру m x 2, з тією різницею, що необхідно визначати не нижню величину виграшу, а верхню і знаходити не максимальне з можливих значення, а мінімальне.