- Цветы и растения
- Аквариум и рыбы
- Для работы
- Для сайта
- Для обучения
- Почтовые индексы Украины
- Всяко-разно
- Электронные библиотеки
- Реестры Украины
- Старинные книги о пивоварении
- Словарь старославянских слов
- Все романы Пелевина
- 50 книг для детей
- Стругацкие, сочинения в 33 томах
- Записи Леонардо да Винчи
- Биология поведения человека
Главная  Прочие дисциплины Прочие дисциплины  Книги Книги  Математичне програмування - Наконечний С.І. Математичне програмування - Наконечний С.І. |
Математичне програмування - Наконечний С.І.
6.7. Приклади застосування цілочислових задач лінійного програмування у плануванні та управлінні виробництвом
Задача про рюкзак. Найпростішою задачею цілочислового програмування, а саме задачею лише з одним обмеженням, є задача про рюкзак (або ранець). Така задача має багато прикладів практичного застосування. Назва «задача про рюкзак» пов’язана з інтерпретацією задачі вибору найкращого складу предметів, що задовольняють певні умови гіпотетичної проблеми туриста щодо вибору для походу оптимальної кількості речей.
Турист може вибирати потрібні речі із списку з n предметів. Відома вага кожного j-го предмета  . Визначена також цінність кожного виду предметів
. Визначена також цінність кожного виду предметів  . Максимальна вага всього вантажу в рюкзаку не може перевищувати зазначеного обсягу М. Необхідно визначити, скільки предметів кожного виду турист має покласти в рюкзак, щоб загальна цінність спорядження була максимальною за умови виконання обмеження на вагу рюкзака.
. Максимальна вага всього вантажу в рюкзаку не може перевищувати зазначеного обсягу М. Необхідно визначити, скільки предметів кожного виду турист має покласти в рюкзак, щоб загальна цінність спорядження була максимальною за умови виконання обмеження на вагу рюкзака.
Позначимо через  – кількість предметів j-го виду в рюкзаку. Тоді математична модель задачі матиме вигляд:
– кількість предметів j-го виду в рюкзаку. Тоді математична модель задачі матиме вигляд:

 ;
;
 ,
,  — цілі числа,
— цілі числа,  .
.
 Фермеру для удобрення земельної ділянки необхідно придбати 107 кг добрив. Він може купити добрива в упаковках по 35 кг вартістю 14 ум. од. або по 24 кг вартістю 12 ум. од. Метою фермера є закупівля не менше, ніж 107 кг добрив з мінімальними витратами. Причому потрібно купувати або цілу упаковку, або не купувати її зовсім, бо частину упаковки придбати неможливо.
Фермеру для удобрення земельної ділянки необхідно придбати 107 кг добрив. Він може купити добрива в упаковках по 35 кг вартістю 14 ум. од. або по 24 кг вартістю 12 ум. од. Метою фермера є закупівля не менше, ніж 107 кг добрив з мінімальними витратами. Причому потрібно купувати або цілу упаковку, або не купувати її зовсім, бо частину упаковки придбати неможливо.
Розв’язання. Позначимо кількість упаковок вагою 35 кг та вагою 24 кг відповідно змінними  та
та  . Маємо модель цієї задачі:
. Маємо модель цієї задачі:

 ;
;
 ,
,  — цілі числа.
— цілі числа.
У результаті розв’язування задачі будь-яким з вищенаведених методів отримаємо оптимальний план:  ,
,  . Отже, за оптимальним планом найменші витрати, що дорівнюють 50 ум. од., можливі у разі закупівлі однієї упаковки добрив вагою 35 кг та трьох вагою по 24 кг.
. Отже, за оптимальним планом найменші витрати, що дорівнюють 50 ум. од., можливі у разі закупівлі однієї упаковки добрив вагою 35 кг та трьох вагою по 24 кг.
Задача оптимального розкрою матеріалів. На підприємстві здійснюється розкрій m різних партій матеріалів у обсягах  одиниць однакового розміру в кожній партії. Із матеріалів усіх партій потрібно виготовити максимальну кількість комплектів Z, у кожен з яких входить p різних видів окремих частин в кількості
одиниць однакового розміру в кожній партії. Із матеріалів усіх партій потрібно виготовити максимальну кількість комплектів Z, у кожен з яких входить p різних видів окремих частин в кількості  одиниць, враховуючи, що кожну одиницю матеріалу можна розкроїти на окремі частини n різними способами, причому у разі розкрою одиниці i-ої партії j-им способом отримуємо
одиниць, враховуючи, що кожну одиницю матеріалу можна розкроїти на окремі частини n різними способами, причому у разі розкрою одиниці i-ої партії j-им способом отримуємо  деталей r-го виду.
деталей r-го виду.
Запишемо математичну модель задачі. Позначимо через  — кількість одиниць матеріалу i-ої партії, що будуть розкроєні j-им способом. Тоді з i-ої партії за j-го способу розкрою отримаємо
— кількість одиниць матеріалу i-ої партії, що будуть розкроєні j-им способом. Тоді з i-ої партії за j-го способу розкрою отримаємо 
 деталей r-го виду. З усієї ж i-ої партії у разі застосування до неї всіх n способів розкрою отримаємо
деталей r-го виду. З усієї ж i-ої партії у разі застосування до неї всіх n способів розкрою отримаємо  деталей r-го виду, а з усіх m партій їх буде отримано
деталей r-го виду, а з усіх m партій їх буде отримано  . У кожен комплект має входити
. У кожен комплект має входити  деталей, тому відношення
деталей, тому відношення  визначає кількість комплектів, які можна виготовити з деталей r-го виду. Кількість повних комплектів для всіх видів деталей визначається найменшим з цих відношень.
визначає кількість комплектів, які можна виготовити з деталей r-го виду. Кількість повних комплектів для всіх видів деталей визначається найменшим з цих відношень.
У разі повного комплекту має виконуватися рівність відношень:
 ,
,
звідки p – 1 відношення можна виразити через будь-яке з них, наприклад, через перше:

 або
або 
 .
.
Замінивши  та
та  їх значеннями, отримаємо p – 1 обмеження стосовно комплектів:
їх значеннями, отримаємо p – 1 обмеження стосовно комплектів:
 ;
;

Враховуючи наявну кількість одиниць матеріалу в партіях, запишемо m обмежень щодо ресурсів:
 .
.
(Обмеження щодо використання ресурсів можуть бути рівняннями чи нерівностями залежно від того, повністю чи не повністю необхідно використати наявний обсяг ресурсів).
Всі  мають задовольняти умову невід’ємності:
мають задовольняти умову невід’ємності:  та цілочисловості.
та цілочисловості.
Отже, необхідно знайти найбільше значення функції:

за обмежень:

 ,
,
 — цілі числа
— цілі числа  .
.
Розглянемо приклад задачі оптимального розкрою матеріалів.
 У цеху розрізують прути завдовжки 6 м на заготівки довжиною 1,4, 2 і 2,5 м. Цех обслуговує двох замовників, для кожного з яких окремо необхідно знайти:
У цеху розрізують прути завдовжки 6 м на заготівки довжиною 1,4, 2 і 2,5 м. Цех обслуговує двох замовників, для кожного з яких окремо необхідно знайти:
- як розрізати 200 прутів, щоб отримати не менше як 40, 60 і 50 заготівок завдовжки відповідно 1,4; 2 і 2,5 м. Критерій оптимізації — мінімум відходів;
- як розрізати 200 прутів для формування з отриманих заготівок комплектів, що складаються з двох заготівок довжиною 1,4 м, та по одній довжиною 2 і 2,5 м. Критерій оптимізації – максимальна кількість комплектів.
Розв’язання.
1) розв’яжемо задачу за умовами першого замовника. Маємо партію прутів у кількості  штук. Відома нижня межа кількості заготівок кожного виду. Введемо такі позначення:
штук. Відома нижня межа кількості заготівок кожного виду. Введемо такі позначення:
 — вид заготівки;
— вид заготівки;
 — спосіб розрізання прута;
— спосіб розрізання прута;
 — вихід у разі розрізування прута j-им способом заготівок r-го виду;
— вихід у разі розрізування прута j-им способом заготівок r-го виду;
cj — відходи в разі розрізування прута j-им способом;
 — кількість наявних прутів;
— кількість наявних прутів;
Dr — нижня межа потреби в r-ій заготівці;
xj — кількість прутів, які розрізані за j-им способом.
Запишемо математичну модель для розв’язування першого пункту задачі оптимального розкрою.
Критерієм оптимальності є мінімальна кількість відходів:  .
.
Кількість отриманих заготівок кожного виду має бути не меншою від зазначених потреб:

Сумарна кількість прутів, які розрізані різними способами не може бути більшою від кількості наявних прутів:
 .
.
Змінні задачі  — невід’ємні і цілі числа. Отже, маємо математичну модель:
— невід’ємні і цілі числа. Отже, маємо математичну модель:


 ,
,
 — цілі числа
— цілі числа  .
.
Побудуємо числову економіко-математичну модель розрізування прутів, розглянувши можливі варіанти їх розрізування:
Таблиця 6.5
| Довжина заготівки, м | Варіант розрізування прутів | ||||||
x1 | x2 | x3 | x4 | x5 | x6 | x7 | |
1,4 | 4 | — | — | 1 | 1 | 2 | 2 |
2 | — | 3 | — | 1 | 2 | 1 | — |
2,5 | — | — | 2 | 1 | — | — | 1 |
Довжина відходів, м | 0,4 | 0 | 1 | 0,1 | 0,6 | 1,2 | 0,7 |
Бажано, щоб у множину ввійшли всі можливі варіанти, навіть такі, які на перший погляд здаються неефективними, наприклад, Х6.
Запишемо числову економіко-математичну модель розрізування прутів:

за умов:
а) кількість заготівок завдовжки 1,4 м:
 ;
;
б) кількість заготівок завдовжки 2 м:
 ;
;
в) кількість заготівок завдовжки 2,5 м:
 ;
;
г) кількість наявних прутів:
 ;
;
д) невід’ємність змінних:
 ;
;
є) цілочисловість змінних:
 — цілі числа
— цілі числа  .
.
Отже, загалом маємо математичну модель виду:


 ,
,
 — цілі числа
— цілі числа  .
.
Розв’язуючи задачу одним із методів цілочислового програмування, отримуємо набір альтернативних оптимальних планів (загальною кількістю 146). Наприклад, такий план забезпечує виготовлення всіх видів заготівок у мінімально можливій кількості за найменшого загального обсягу відходів, причому для цього використовуються лише 54 прути: 
 ,
,  , тобто 4 прути необхідно розрізати другим способом (по три заготівки довжиною 2 м) та 50 прутів четвертим способом (по одній заготівці кожного виду). Сумарна довжина залишків дорівнює п’яти метрам. Аналогічне значення цільової функції (
, тобто 4 прути необхідно розрізати другим способом (по три заготівки довжиною 2 м) та 50 прутів четвертим способом (по одній заготівці кожного виду). Сумарна довжина залишків дорівнює п’яти метрам. Аналогічне значення цільової функції ( ) дає оптимальний план, за яким виготовляється більша кількість кінцевої продукції та витрачається весь наявний матеріал:
) дає оптимальний план, за яким виготовляється більша кількість кінцевої продукції та витрачається весь наявний матеріал:
 .
.
Отримані оптимальні плани дають набір альтернативних варіантів для прийняття управлінських рішень за конкретних виробничих умов.
Ускладнимо розглянутий приклад задачі оптимального розкрою матеріалів, що передбачає тільки один тип матеріалу та відсутність формування комплектів кінцевої продукції.
2) розв’яжемо задачу за умовами другого замовника. Оскільки в другому пункті задачі відсутні обмеження щодо кількості заготівок, проте вимагається формування комплектів, необхідно дещо змінити позначення:
 — вид заготівки;
— вид заготівки;
 — спосіб розрізування прута;
— спосіб розрізування прута;
 — вихід у разі розрізування прута j-им способом заготівок r-го виду;
— вихід у разі розрізування прута j-им способом заготівок r-го виду;
 — кількість наявних прутів;
— кількість наявних прутів;
xj — кількість прутів, які розрізані за j-им варіантом;
 — кількість r-го виду заготівок у комплекті;
— кількість r-го виду заготівок у комплекті;
 — кількість всіх заготівок r-го виду.
— кількість всіх заготівок r-го виду.
Математична модель у цьому разі суттєво відрізняється від моделі, що розглянута вище.
З усього матеріалу може бути отримано  заготівок r-го виду. У кожен комплект має входити дві заготівки першого типу
заготівок r-го виду. У кожен комплект має входити дві заготівки першого типу  , тому відношення
, тому відношення  визначає кількість комплектів, які можна скласти з заготівок першого виду. Аналогічно можна визначити кількість комплектів для інших видів заготівок
визначає кількість комплектів, які можна скласти з заготівок першого виду. Аналогічно можна визначити кількість комплектів для інших видів заготівок  та
та  . Кількість можливих повних комплектів визначається найменшим з цих відношень:
. Кількість можливих повних комплектів визначається найменшим з цих відношень:  . До того ж у разі повного комплекту має виконуватися рівність відношень:
. До того ж у разі повного комплекту має виконуватися рівність відношень:  , звідки два з відношень можна виразити, наприклад, через перше:
, звідки два з відношень можна виразити, наприклад, через перше:
 , звідки
, звідки  ,
,  .
.
Замінимо  та
та  їх значеннями:
їх значеннями:
 або
або  ;
;
 або
або  .
.
Враховуючи наявну кількість одиниць матеріалу, запишемо обмеження щодо використання ресурсів:
 .
.
Всі  мають задовольняти умову невід’ємності:
мають задовольняти умову невід’ємності: 
 та цілочисловості.
та цілочисловості.
Отже, необхідно знайти найбільше значення функції:

за обмежень:

 ,
,
 — цілі числа
— цілі числа  .
.
Запишемо числову математичну модель, скориставшись попередніми даними розрахунків можливих варіантів розрізування прутів (табл. 6.5).
Із умов формування комплектів маємо: 
 , тобто заготівок першого виду має бути вдвічі більше, ніж заготівок другого та третього виду. Звідси випливає, що за мінімальну кількість комплектів може бути прийняте одне з двох відношень:
, тобто заготівок першого виду має бути вдвічі більше, ніж заготівок другого та третього виду. Звідси випливає, що за мінімальну кількість комплектів може бути прийняте одне з двох відношень:  чи
чи  . Виберемо, наприклад,
. Виберемо, наприклад,  . Використовуючи дані таблиці, запишемо вираз для цільової функції:
. Використовуючи дані таблиці, запишемо вираз для цільової функції:
 .
.
Обмеження щодо формування комплектів матимуть вигляд:  , або
, або
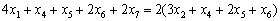 ,
,
звідси
 ,
,
аналогічно для  :
:
 , або
, або
 .
.
Обмеження щодо використання наявних прутів:
 .
.
Обмеження стосовно невід’ємності та цілочисловості змінних:
 ;
;
 — цілі числа
— цілі числа  .
.
Отже, загалом маємо таку математичну модель:
max 


 — цілі числа
— цілі числа  .
.
Розв’язавши задачу будь-яким з вищеописаних методів, отримаємо оптимальний план: 
 ,
,
 комплектів.
комплектів.
Задача комівояжера. Розглядається n міст А1, А2,..., Аn, що пов’язані між собою транспортною мережею. Відома матриця відстаней від кожного міста до усіх інших:
 ,
,
причому в загальному випадку не завжди  . Комівояжер повинен побувати в кожному місті тільки один раз і повернутися в те місто, з якого почав рухатися. Необхідно відшукати такий замкнений маршрут, що проходить через кожне місто лише один раз і довжина якого мінімальна.
. Комівояжер повинен побувати в кожному місті тільки один раз і повернутися в те місто, з якого почав рухатися. Необхідно відшукати такий замкнений маршрут, що проходить через кожне місто лише один раз і довжина якого мінімальна.
Позначимо:

Отже, хij може набувати лише двох значень: одиниці або нуля. Такі змінні мають назву бульових змінних. Очевидно, що вони є цілочисловими. Цільовою функцією цієї задачі є мінімізація всього маршруту комівояжера:
 ,
,
де сij — відстань між містами і та j.
Обмеження щодо одноразового в’їзду в кожне місто:

 .
.
Обмеження щодо одноразового виїзду з кожного міста:

 .
.
Зазначені обмеження не повністю описують допустимі маршрути і не виключають можливості розриву маршруту. Щоб усунути цей недолік, введемо невід’ємні цілочислові змінні 
 , які в процесі розв’язування задачі набуватимуть значень порядкових номерів міст за оптимальним маршрутом прямування комівояжера. Запишемо обмеження, які усувають можливість існування підмаршрутів:
, які в процесі розв’язування задачі набуватимуть значень порядкових номерів міст за оптимальним маршрутом прямування комівояжера. Запишемо обмеження, які усувають можливість існування підмаршрутів:

 .
.
Доведемо, що для довільного маршруту, який починається в пункті А1, можна знайти такі  , що задовольняють наведену нерівність. Нехай комівояжер переїжджає з міста Аі до міста Аj на р-му кроці і допустимо також, що
, що задовольняють наведену нерівність. Нехай комівояжер переїжджає з міста Аі до міста Аj на р-му кроці і допустимо також, що  , тоді з міста Аj комівояжер вирушить на наступному, (р + 1)-му кроці і
, тоді з міста Аj комівояжер вирушить на наступному, (р + 1)-му кроці і  . Звідси випливає, що:
. Звідси випливає, що:
 .
.
Така нерівність виконується для будь-яких значень i та j у разі, коли  , а при
, а при  нерівність виконується як строге рівняння. Отже, якщо вибрано маршрут пересування з i-го міста до j-го, то згадана нерівність фіксує два підряд порядкових номери цих міст.
нерівність виконується як строге рівняння. Отже, якщо вибрано маршрут пересування з i-го міста до j-го, то згадана нерівність фіксує два підряд порядкових номери цих міст.
Отже, маємо таку математичну модель:



 В економічному регіоні розміщено 6 пунктів (міст). Комівояжер, який виїжджає з міста 1, має побувати в кожному місті один раз і повернутися до вихідного пункту. Знайти найкоротший маршрут, якщо відстані між містами відомі (наведені в км на рис. 6.7).
В економічному регіоні розміщено 6 пунктів (міст). Комівояжер, який виїжджає з міста 1, має побувати в кожному місті один раз і повернутися до вихідного пункту. Знайти найкоротший маршрут, якщо відстані між містами відомі (наведені в км на рис. 6.7).

Рис. 6.7
Розв’язання. Маємо 6 пунктів, де має побувати комівояжер.
Позначимо:

Отже, хij — бульові (цілочислові) змінні. Запишемо числову економіко-математичну модель задачі комівояжера за даних умов.
Виходячи з рис. 6.5, висновуємо, що всіх можливих маршрутів є 12. З першого міста можна потрапити до кожного з інших п’яти, відповідні маршрути позначимо змінними  ,
,  ,
,  ,
,  ,
,  . Друге місто пов’язане лише з трьома іншими, а саме, з першим, четвертим та п’ятим, отже, маємо такі три змінні:
. Друге місто пов’язане лише з трьома іншими, а саме, з першим, четвертим та п’ятим, отже, маємо такі три змінні:  ,
,  ,
,  . Аналогічно позначаємо змінні, що відповідають можливим маршрутам пересувань з третього, четвертого, п’ятого та шостого міст:
. Аналогічно позначаємо змінні, що відповідають можливим маршрутам пересувань з третього, четвертого, п’ятого та шостого міст:
з третього —  ,
,  ,
,  ,
,
з четвертого —  ,
,  ,
,  ,
,  ,
,  ,
,
з п’ятого —  ,
,  ,
,  ,
,  ,
,
з шостого —  ,
,  ,
,  ,
,  .
.
Загалом отримали 24 змінні. Однак деякі змінні, наприклад,  та
та  ,
,  та
та  описують один маршрут, довжина якого за умовою задачі не змінюється залежно від напрямку пересування (у разі переїзду з першого міста до другого чи з другого до першого необхідно подолати 50 км). Отже, коефіцієнт у цільовій функції при таких змінних буде однаковим.
описують один маршрут, довжина якого за умовою задачі не змінюється залежно від напрямку пересування (у разі переїзду з першого міста до другого чи з другого до першого необхідно подолати 50 км). Отже, коефіцієнт у цільовій функції при таких змінних буде однаковим.
Критерій оптимальності — мінімізація довжини всього маршруту комівояжера:


 ;
;
а) обмеження щодо одноразового в’їзду в кожне місто:






б) обмеження щодо одноразового виїзду з кожного міста:

 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
в) обмеження щодо усунення підмаршрутів:
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;

ui(uj) — цілі числа  .
.
Такі задачі розв’язуються спеціальними методами.
 У результаті отримуємо оптимальний варіант пересування таким маршрутом (рис. 6.8).
У результаті отримуємо оптимальний варіант пересування таким маршрутом (рис. 6.8).
Тобто з першого міста за оптимальним планом необхідно переїжджати до четвертого, з четвертого — до третього, з третього — до шостого, з шостого — до п’ятого, з п’ятого — до другого, а з другого — до першого. Довжина цього маршруту, яка є мінімальною, дорівнює 300 км.
Зауважимо, що аналогічні задачі нерідко виникають на практиці, особливо у дрібному бізнесі. Типовим може бути, наприклад, таке завдання: «Фірма у місті має 25 кіосків, які торгують безалкогольними напоями. Щоденно з бази автомобілем розвозять до них товар. Як оптимально організувати розвезення певного обсягу товару?».
Задача з постійними елементами витрат. Відомо, що витрати на виготовлення будь-якої продукції складаються з двох частин: постійних та змінних витрат.
Нехай розглядається процес виробництва продукції за умов використання m видів ресурсів. Відомі обсяги кожного виду ресурсів  , а також норми використання i-го
, а також норми використання i-го  виду ресурсів на одиницю виготовлення j-го
виду ресурсів на одиницю виготовлення j-го  виду продукції
виду продукції  .
.
Умови використання ресурсів на виготовлення продукції можна записати у вигляді таких обмежень:
 .
.
Витрати на виготовлення продукції поділяють на два види: постійні витрати —  , які не залежать від обсягу виробництва, і змінні — сj, що розраховуються на одиницю виготовленої продукції, де j — вид продукції. Необхідно визначити оптимальні обсяги виробництва продукції
, які не залежать від обсягу виробництва, і змінні — сj, що розраховуються на одиницю виготовленої продукції, де j — вид продукції. Необхідно визначити оптимальні обсяги виробництва продукції  , за яких загальні витрати були б мінімальними.
, за яких загальні витрати були б мінімальними.
Зауважимо, що виготовлення будь-якої кількості продукції  потребує певних фіксованих
потребує певних фіксованих  та змінних
та змінних  витрат, тобто загальна сума витрат на виготовлення продукції обсягом
витрат, тобто загальна сума витрат на виготовлення продукції обсягом  визначається за формулою:
визначається за формулою:  . Однак у разі, якщо
. Однак у разі, якщо  (продукція не випускається), то розрахунок витрат за формулою
(продукція не випускається), то розрахунок витрат за формулою  призводить до додатного значення, що неправильно. Для адекватного відображення функціональної залежності загальних витрат від обсягу виробленої продукції j-го виду можна скористатися такою нелінійною функцією:
призводить до додатного значення, що неправильно. Для адекватного відображення функціональної залежності загальних витрат від обсягу виробленої продукції j-го виду можна скористатися такою нелінійною функцією:
 ,
,
де  є бульовими змінними виду:
є бульовими змінними виду:
Таку умову можна записати у вигляді лінійної нерівності. Допустимо, що існує таке досить велике число М, для якого умова  виконуватиметься для всіх допустимих значень
виконуватиметься для всіх допустимих значень  . Тоді обмеження виду:
. Тоді обмеження виду:

завжди виконується при  , і, крім того, якщо
, і, крім того, якщо  – ціле число, то мінімізація цільової функції забезпечує найменше значення
– ціле число, то мінімізація цільової функції забезпечує найменше значення  . Якщо
. Якщо  , то нерівність
, то нерівність  забезпечить
забезпечить  .
.
Отже, маємо таку математичну модель:
цільова функція, що описує мінімальні загальні витрати на виробництво всіх видів продукції, набуває вигляду:

за умов:

 ;
;
 ;
;
 — цілі числа
— цілі числа  .
.
 Фермер планує виробляти три види продукції: озиму пшеницю, цукрові буряки та молоко. Загальні витрати складаються з двох частин: постійних та змінних. Відповідні дані наведені в табл. 6.6:
Фермер планує виробляти три види продукції: озиму пшеницю, цукрові буряки та молоко. Загальні витрати складаються з двох частин: постійних та змінних. Відповідні дані наведені в табл. 6.6:
Таблиця 6.6
Показник | Вид продукції | ||
озима пшениця | цукрові буряки | молоко | |
Постійні витрати, тис. грн | 40 | 70 | 20 |
Змінні витрати на одиницю продукції, грн/т | 400 | 150 | 500 |
Норма потреби в ріллі, га/т | 0,2 | 0,02 | 0,25 |
Ціна одиниці продукції, грн/т | 800 | 300 | 1000 |
Необхідно визначити оптимальний план виробництва продукції кожного виду за умови, що фермер має 100 га ріллі.
Розв’язання. Нехай хj — обсяг виробництва j-го виду продукції m,  .
.
Функція загальних витрат на виробництво j-го виду продукції має вигляд:
 .
.
Цільовою функцією в цьому прикладі може бути максимізація прибутку:
 ,
,
де рj — ціна одиниці j-ї продукції.
Обмеження щодо використання ріллі запишемо так:
 ,
,
де аj — норма потреби у ріллі на виробництво одиниці j-ї продукції; А — площа ріллі.
Загалом маємо таку математичну модель:


 ;
;
 ;
;
 — цілі числа
— цілі числа  .
.
Запишемо числову економіко-математичну модель цієї задачі. Очевидно, що максимально можливий обсяг виробництва пшениці становить =500 т, цукрових буряків —
=500 т, цукрових буряків —  =5000 т, молока —
=5000 т, молока — =400 т. Отже, М може дорівнювати 5000. Звідси маємо:
=400 т. Отже, М може дорівнювати 5000. Звідси маємо:
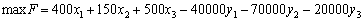
за умов:
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 — цілі числа
— цілі числа  .
.
Розв’язавши задачу, отримаємо оптимальний план:
 .
.  .
.
Можна висновувати, що фермеру за цих умов найвигідніше зайнятися вирощуванням на всій площі ріллі тільки цукрових буряків.
Звичайно, у реальній ситуації існує більший набір можливих видів продукції, а також більше обмежень щодо використання ресурсів.
Задача планування виробничої лінії. Розглядається процес функціонування виробничої лінії. Відома схема, яка зображає послідовність робіт для виготовлення k видів продукції  . Відомі також: aj — тривалість виконання j-ї операції
. Відомі також: aj — тривалість виконання j-ї операції  ;
;  — термін для k-го виробу, до якого необхідно завершити операцію j; хj — момент початку j-ї операції; t — тривалість виконання всіх операцій. Допускається, що в будь-який момент на верстаті виконується тільки одна операція.
— термін для k-го виробу, до якого необхідно завершити операцію j; хj — момент початку j-ї операції; t — тривалість виконання всіх операцій. Допускається, що в будь-який момент на верстаті виконується тільки одна операція.
Необхідно визначити оптимальні моменти початку кожної операції.
Економіко-математична модель виробничої лінії міститиме такі групи обмежень:
1. Послідовність виконання j-ї операції записується для всіх пар операцій так: 
 якщо j-та операція передує i-й операції.
якщо j-та операція передує i-й операції.
2. Обмеження щодо нерозгалуженості виробничого процесу для операцій і та j, які не виконуються одночасно (i ≠ j), має вигляд:
або xi – хj = aj, якщо операція j передує операції і;
або xj –хi = ai, якщо операція і передує операції j.
Зауважимо, що логічні обмеження виду «або-або» не можуть входити до економіко-математичної моделі задачі лінійного програмування, оскільки вони породжують неопуклу множину допустимих розв’язків. Тому необхідно ввести допоміжні змінні, які уможливлюють запис наведених вище логічних умов у вигляді лінійних обмежень. Це такі бульові змінні:

Скориставшись прийомом з попереднього прикладу 6.6. (введення досить великого числа М), запишемо обмеження:

 ;
;

 ,
,
де М — досить велике число.
3. Обмеження щодо термінів виготовлення кожного виробу:

 ,
,
де j — остання операція для k-го виробу.
4. Усі операції мають бути виконані до моменту t:
 ,
, .
.
Критерій оптимальності:
 ,
,
тобто ставиться завдання, щоб тривалість виготовлення всіх видів виробів була мінімальною.
Отже, маємо таку математичну модель:



 ,
,  — цілі числа
— цілі числа  .
.
 Потрібно оптимізувати функціонування виробничої лінії, яка охоплює 11 операцій з виготовлення двох виробів. Лінію обладнано одним багатоопераційним верстатом. Послідовність і тривалість (у хвилинах) виконання операцій відображені на рис. 6.9.
Потрібно оптимізувати функціонування виробничої лінії, яка охоплює 11 операцій з виготовлення двох виробів. Лінію обладнано одним багатоопераційним верстатом. Послідовність і тривалість (у хвилинах) виконання операцій відображені на рис. 6.9.

Рис. 6.9
Визначені тривалості виготовлення виробів А та В відповідно дорівнюють 120 і 150 хв. Передбачається, що в кожний момент часу на верстаті може виконуватися тільки одна операція. Визначити оптимальні моменти початку кожної операції.
Розв’язання. Позначивши через хj момент початку j-ої операції, запишемо числову економіко-математичну модель функціонування виробничої лінії:

за наведених нижче умов.
1. Обмеження стосовно послідовності виконання операцій:
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
2. Обмеження щодо нерозгалуженості виробничого процесу:
 ;
;
 ;
;
 ;
;
 ;
;
.........................................
 ;
;
 ;
;
...........................................
 ;
;
 .
.
3. Обмеження щодо тривалостей виготовлення виробів:
 ;
;
 .
.
4. Усі операції мають бути виконані до моменту t:
 ;
;
 ;
;
 ;
;
...................
 ;
;
..................
 .
.
5. Обмеження щодо невід’ємності змінних:
 ;
;
 ,
,  — цілі
— цілі  .
.
Отже, маємо частково цілочислову задачу з бульовими змінними.
Задача про призначення. Ця задача була розглянута в розділі 5 як така, що зводиться до транспортної і може бути розв’язана одним з відомих методів знаходження оптимального плану транспортної задачі. Проте такий вид задач належить до задач цілочислового програмування, оскільки їх змінні є бульовими і оптимальний план може бути знайденим також методами цілочислового програмування. Не повертаючись до загальної постановки задачі та побудови її математичної моделі (див. § 5.10), наведемо ще один приклад задачі про призначення.
 Необхідно розподілити чотирьох робітників за чотирма видами устаткування так, щоб їх загальна продуктивність праці була максимальною. Дані стосовно продуктивності праці кожного робітника на устаткуванні кожному виду наведено в табл. 6.7:
Необхідно розподілити чотирьох робітників за чотирма видами устаткування так, щоб їх загальна продуктивність праці була максимальною. Дані стосовно продуктивності праці кожного робітника на устаткуванні кожному виду наведено в табл. 6.7:
Таблиця 6.7
Робітник | Продуктивність праці на устаткуванні, грн/год | |||
1 | 2 | 3 | 4 | |
1 | 12 | 9 | 8 | 7 |
2 | 10 | 7 | 6 | 5 |
3 | 9 | 6 | 4 | 4 |
4 | 8 | 5 | 3 | 2 |
Розв’язання. Зазначимо, що дану задачу можна розглядати як транспортну, в якій робітники ототожнюються з постачальниками вантажів, а види устаткування — зі споживачами цих вантажів. Обсяги пропозиції та попиту в кожному разі дорівнюють одиниці. Отже, змінні будуть бульовими:

Якщо відома продуктивність праці і-го робітника на j-му устаткуванні, то числова модель про призначення набуває вигляду:


за умов:
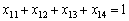 ;
;
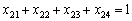 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.

 ;
;
 — цілі числа
— цілі числа  .
.
З огляду на особливу структуру цієї задачі, зокрема на її «транспортний» характер та рівність правих частин обмежень, для її розв’язування можна застосувати ефективніший алгоритм, ніж для звичайної задачі цілочислового програмування з бульовими змінними. Пропонуємо читачеві ознайомитися з такими алгоритмами, які детально описані в літературі [12].
Created/Updated: 25.05.2018
 |
|