- Цветы и растения
- Аквариум и рыбы
- Для работы
- Для сайта
- Для обучения
- Почтовые индексы Украины
- Всяко-разно
- Электронные библиотеки
- Реестры Украины
- Старинные книги о пивоварении
- Словарь старославянских слов
- Все романы Пелевина
- 50 книг для детей
- Стругацкие, сочинения в 33 томах
- Записи Леонардо да Винчи
- Биология поведения человека
Главная  Прочие дисциплины Прочие дисциплины  Книги Книги  Математичне програмування - Наконечний С.І. Математичне програмування - Наконечний С.І. |
Математичне програмування - Наконечний С.І.
6.5. Комбінаторні методи. Метод гілок та меж
В основі комбінаторних методів є перебір можливих варіантів розв’язків поставленої задачі. Кожен з них характеризується певною послідовністю перебору варіантів та правилами виключення, що дають змогу ще в процесі розв’язування задачі виявити неоптимальні варіанти без попередньої їх перевірки. Відносна ефективність різних методів залежить від того, наскільки кожен з них уможливлює скорочення необхідного процесу перебору варіантів у результаті застосування правила виключення.
Розглянемо один із комбінаторних методів. Для розв’язування задач цілочислового програмування ефективнішим за метод Гоморі є метод гілок і меж. Спочатку, як і в разі методу Гоморі, симплексним методом розв’язується послаблена (без умов цілочисловості) задача. Потім вводиться правило перебору.
Нехай потрібно знайти хj — цілочислову змінну, значення якої хj= в оптимальному плані послабленої задачі є дробовим. Очевидно, що в деякому околі даної точки також не існує цілочислових значень, тому відповідний проміжок можна виключити з множини допустимих планів задачі в подальшому розгляді. Таким проміжком є інтервал між найближчими до
в оптимальному плані послабленої задачі є дробовим. Очевидно, що в деякому околі даної точки також не існує цілочислових значень, тому відповідний проміжок можна виключити з множини допустимих планів задачі в подальшому розгляді. Таким проміжком є інтервал між найближчими до  цілочисловими значеннями. Можна стверджувати, що на інтервалі
цілочисловими значеннями. Можна стверджувати, що на інтервалі  цілих значень немає.
цілих значень немає.
Наприклад, якщо  =2,7 дістаємо інтервал
=2,7 дістаємо інтервал  , де, очевидно, немає хj, яке набуває цілого значення і оптимальний розв’язок буде знаходитися або в інтервалі
, де, очевидно, немає хj, яке набуває цілого значення і оптимальний розв’язок буде знаходитися або в інтервалі  , або
, або  . Виключення проміжку
. Виключення проміжку  з множини допустимих планів здійснюється введенням до системи обмежень початкової задачі додаткових нерівностей. Тобто допустиме ціле значення xj має задовольняти одну з нерівностей виду:
з множини допустимих планів здійснюється введенням до системи обмежень початкової задачі додаткових нерівностей. Тобто допустиме ціле значення xj має задовольняти одну з нерівностей виду:
 або
або  .
.
Дописавши кожну з цих умов до задачі з послабленими обмеженнями, дістанемо дві, не пов’язані між собою, задачі. Тобто, початкову задачу цілочислового програмування (6.1)—(6.4) поділимо на дві задачі з урахуванням умов цілочисловості змінних, значення яких в оптимальному плані послабленої задачі є дробовими. Це означає, що симплекс-методом розв’язуватимемо дві такі задачі:
перша задача:  (6.14)
(6.14)
за умов:

 ; (6.15)
; (6.15)

 ; (6.16)
; (6.16)
 — цілі числа,
— цілі числа,  ; (6.17)
; (6.17)
 , (6.18)
, (6.18)
друга задача
 (6.19)
(6.19)
за умов:
 ,
,  ; (6.20)
; (6.20)

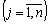 ; (6.21)
; (6.21)
 — цілі числа
— цілі числа  ; (6.22)
; (6.22)
 , (6.23)
, (6.23)
де  — дробова компонента розв’язку задачі (6.1)—(6.4).
— дробова компонента розв’язку задачі (6.1)—(6.4).
Наведені задачі (6.14)—(6.18) і (6.19)—(6.23) спочатку послаблюємо, тобто розв’язуємо з відкиданням обмежень (6.17) і (6.22). Якщо знайдені оптимальні плани задовольняють умови цілочисловості, то ці плани є розв’язками задачі (6.1)—(6.4). Інакше пошук розв’язку задачі триває. Для дальшого розгалуження вибираємо розв’язок задачі з більшим значенням цільової функції, якщо йдеться про максимізацію, і навпаки — з меншим значенням цільової функції в разі її мінімізації. Подальше розгалуження виконується доти, доки не буде встановлено неможливість поліпшення розв’язку. Здобутий останній план — оптимальний.
Розв’язування цілочислових задач методом гілок і меж можна значно прискорити. Очевидно, що кожна наступна задача, яку отримують в процесі розв’язування відрізняється від попередньої лише одним обмеженням. Тому за послідовного розв’язування задач немає сенсу розв’язувати їх симплексним методом спочатку. Досить буде почергово приєднати нові обмеження виду (6.18) і (6.23) до останньої симплекс-таблиці попередньої задачі та вилучити (в разі необхідності) непотрібні «старі» обмеження.
 Геометрично введення додаткових лінійних обмежень виду (6.18) та (6.23) в систему обмежень початкової задачі означає проведення гіперплощин (прямих), що розтинають багатогранник (багатокутник) допустимих планів відповідної задачі лінійного програмування у такий спосіб, що уможливлюється включення в план найближчої цілої точки цього багатокутника (рис. 6.4). Допустимо, що А — точка максимуму, тоді за методом гілок та меж багатокутник допустимих планів задачі ABCOD поділяється на дві частини прямими
Геометрично введення додаткових лінійних обмежень виду (6.18) та (6.23) в систему обмежень початкової задачі означає проведення гіперплощин (прямих), що розтинають багатогранник (багатокутник) допустимих планів відповідної задачі лінійного програмування у такий спосіб, що уможливлюється включення в план найближчої цілої точки цього багатокутника (рис. 6.4). Допустимо, що А — точка максимуму, тоді за методом гілок та меж багатокутник допустимих планів задачі ABCOD поділяється на дві частини прямими  та
та  +1, що виключає з розгляду точку А, координата якої
+1, що виключає з розгляду точку А, координата якої  є не цілим числом.
є не цілим числом.
Опишемо алгоритм методу гілок та меж:
- Симплексним методом розв’язують задачу (6.1)—(6.3) (без вимог цілочисловості змінних).
Якщо серед елементів умовно-оптимального плану немає дробових чисел, то цей розв’язок є оптимальним планом задачі цілочислового програмування (6.1)—(6.4).
Якщо задача (6.1)—(6.3) не має розв’язку (цільова функція необмежена, або система обмежень несумісна), то задача (6.1)—(6.4) також не має розв’язку.
- Коли в умовно-оптимальному плані є дробові значення, то вибирають одну з нецілочислових змінних
 і визначають її цілу частину
і визначають її цілу частину  .
. - Записують два обмеження, що відтинають нецілочислові розв’язки:
 ,
,
 .
.
- Кожну з одержаних нерівностей приєднують до обмежень початкової задачі. В результаті отримують дві нові цілочислові задачі лінійного програмування.
- У будь-якій послідовності розв’язують обидві задачі. У разі, коли отримано цілочисловий розв’язок хоча б однієї із задач, значення цільової функції цієї задачі зіставляють з початковим значенням. Якщо різниця не більша від заданого числа e, то процес розв’язування може бути закінчено. У разі, коли цілочисловий розв’язок одержано в обох задачах, то з розв’язком початкової зіставляється той, який дає краще значення цільової функції. Якщо ж в обох задачах одержано нецілочислові розв’язки, то для дальшого гілкування вибирають ту задачу, для якої здобуто краще значення цільової функції і здійснюють перехід до кроку 2.
 Розв’яжемо методом гілок і меж задачу з прикладу 6.1.
Розв’яжемо методом гілок і меж задачу з прикладу 6.1.
Розв’язання. Відкинувши умову цілочисловості, дістанемо розв’язок: х1 = 1, х2 =  . Отже, допустиме ціле значення х2 має задовольняти одну з нерівностей
. Отже, допустиме ціле значення х2 має задовольняти одну з нерівностей  або
або  . Приєднуємо до початкової задачі окремо кожне з обмежень, нехтуючи умовою цілочисловості, і розв’язуємо по черзі обидві утворені задачі:
. Приєднуємо до початкової задачі окремо кожне з обмежень, нехтуючи умовою цілочисловості, і розв’язуємо по черзі обидві утворені задачі:
| Задача І | Задача ІІ |
|
|
|
|
|
|
|
|
|
|
|
|
Для задачі І (з обмеженням  ) оптимальним буде розв’язок
) оптимальним буде розв’язок  ,
,  , а для задачі ІІ (з обмеженням
, а для задачі ІІ (з обмеженням  ) — розв’язок
) — розв’язок  ,
,  . Оскільки цілочислового плану не знайдено, процес необхідно продовжити, узявши для дальшого розгалуження першу задачу, оптимальний план якої дає більше значення функціонала. Розв’язуємо задачу І, окремо приєднуючи до неї обмеження:
. Оскільки цілочислового плану не знайдено, процес необхідно продовжити, узявши для дальшого розгалуження першу задачу, оптимальний план якої дає більше значення функціонала. Розв’язуємо задачу І, окремо приєднуючи до неї обмеження:  і
і  . Отримуємо такі дві задачі:
. Отримуємо такі дві задачі:
| Задача ІІІ | Задача ІV |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Розв’язком задачі ІІІ є план  ,
,  , а задачі IV план
, а задачі IV план  ,
,  . Обидва розв’язки є цілочисловими, проте краще значення цільової функції забезпечує розв’язок задачі IV. Тому оптимальним планом початкової цілочислової задачі буде
. Обидва розв’язки є цілочисловими, проте краще значення цільової функції забезпечує розв’язок задачі IV. Тому оптимальним планом початкової цілочислової задачі буде  ,
,  , що збігається з розв’язком, отриманим за методом Гоморі.
, що збігається з розв’язком, отриманим за методом Гоморі.
Схема процесу розв’язування задачі з прикладу 6.1 (рис. 6.5) досить наочно пояснює назву методу гілок та меж. Початкова задача розділяється (гілкується) на дві простіші, і, якщо серед них не існує задачі з цілочисловим оптимальним розв’язком, то процес гілкування продовжується. Отже, всі розглянуті дії можна зобразити у вигляді «дерева»:

Рис. 6.5
Кожен елемент такого «дерева» — це певна задача, що має відповідний оптимальний план. Після одержання нецілочислового розв’язку послабленої (тобто без умови цілочисловості) початкової задачі ми перетворили її на дві інші з додатковими умовами. З них кращим виявився розв’язок задачі І, однак оскільки він був не цілочисловим, то ми продовжили процес гілкування. Задачу І введенням додаткових обмежень перетворили в задачу ІІІ та задачу IV. Оптимальні плани обох цих задач цілочислові, але план задачі IV дає більше значення функціонала, тому цілочисловим оптимальним планом початкової задачі є розв’язок задачі IV.
Коротко розглянемо без наведення прикладів ще один цікавий метод, який можна віднести до типу комбінаторних (його детальний опис є в літературі [12]) — метод послідовного аналізу варіантів. Загальна схема цього методу розроблена українським вченим В. С. Михалевичем, який працював у київському Інституті кібернетики. Ідея цього методу полягає в послідовному повторенні таких процедур:
1) розбиття множини варіантів розв’язків задачі на кілька підмножин, кожна з яких має специфічні властивості;
2) використання вищезазначених властивостей для пошуку логічних суперечностей в опису окремих підмножин;
3) виключення із дальшого розгляду тих підмножин варіантів розв’язків, в описах яких є логічні суперечності.
Отже, методика послідовного аналізу варіантів базується на відсіві неперспективних варіантів ще до їх побудови. Оскільки у разі відсіву неперспективних початкових частин варіантів відсівається і вся процедура продовжень їх розрахунків, то досягається значна економія часу через скорочення обчислювальних операцій. Відсів неперспективних елементів відбувається як за обмеженнями, так і за цільовою функцією. Основа методу послідовного аналізу варіантів полягає у визначенні правила, за яким буде здійснюватися відсів безперспективних значень змінних, у результаті чого постійно звужуватиметься множина значень, для якої відшукують оптимум.
Зрозуміло, що для кожного типу задач цілочислового програмування формулюються специфічні правила для відсіву варіантів.
Метод послідовного аналізу варіантів успішно застосовувався для розв’язування різноманітних задач оптимального планування та проектування. Наприклад, для розрахунку транспортних мереж, розміщення на мережі типу дерева, проектування розподільних електричних мереж, вибору оптимальних параметрів магістральних газопроводів тощо.
Created/Updated: 25.05.2018
 |
| ,
,  ,
,  ;
;  ;
;  ;
;  ;
;  ;
; ;
; ;
;  ;
;  і
і  — цілі числа.
— цілі числа.  і
і  — цілі числа.
— цілі числа.  ,
,  ,
,  ;
;  ;
;  ;
;  ;
;  ;
; ;
; ;
;  ;
;  ;
;  ;
;  і
і  — цілі числа.
— цілі числа.  і
і  — цілі числа.
— цілі числа.