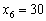Главная Прочие дисциплины Книги Математичне програмування - Наконечний С.І.

Математичне програмування - Наконечний С.І.

4.2. Аналіз розв’язків спряжених економіко-математичних задач

Наведена симплекс-таблиця містить оптимальні плани прямої та двоїстої задач. Оптимальний план прямої задачі позначимо через , а оптимальний план двоїстої — Y*.

Х* = (0; 0; 35; 45; 0; 30; 0), max Z = 285;

Y* = (4; 0; 3) х = (1/2; 0; 2);

min F = 250/2 + 160 = 285 = max Z.

Основні змінні оптимального плану прямої задачі означають обсяги виробництва відповідних видів продукції. Отже, випуск продукції видів А та В не передбачається (х1 = х2 = 0), а С і D — планується у кількості відповідно 35 та 45 од.

Додаткові змінні оптимального плану прямої задачі х5, х6, х7 характеризують залишки (невикористані обсяги) ресурсів відповідно 1, 2 та 3. Оскільки х6 = 30, то це означає, що другий ресурс використовується у процесі виробництва продукції не повністю. Перший та третій ресурси за оптимального плану виробництва будуть використані повністю, бо х5 = х7 = 0.

За такого плану виробництва продукції підприємство отримало б найбільшу виручку обсягом 285 ум. од.

З розділу ІІІ відомо, що між змінними прямої та двоїстої задач існує відповідність виду:

Оптимальний план двоїстої задачі дає оптимальну систему оцінок ресурсів, що використовуються у виробництві.

Основні змінні двоїстої задачі за наведеною схемою відповідають додатковим змінним прямої, що характеризують обсяги невикористаних ресурсів. Отже, отримані значення змінних у1, у2 та у3 можна використати для відносної кількісної оцінки важливості відповідних видів ресурсів. Так, у1 = 1/2 та у3 = 2 відмінні від нуля, а ресурси 1 та 2 (за значеннями додаткових змінних прямої задачі) використовуються повністю. Двоїста оцінка у2 = 0 і відповідний вид ресурсу не повністю використовується за оптимального плану виробництва продукції. Це підтверджується також попереднім аналізом додаткових змінних оптимального плану прямої задачі. Крім того, за третьою теоремою двоїстості відомо: якщо деяка основна змінна оптимального плану двоїстої задачі уі ≠ 0, то зміна (збільшення або зменшення) обсягу відповідного і-го ресурсу приводить до зміни значення цільової функції на величину уі. Якщо уі = 0, то значення цільової функції залишається незмінним.

Отже, у1 = 1/2 означає, що коли запас першого ресурсу збільшити на одну умовну одиницю (b1 = 250 + 1 = 251), то значення цільової функції max Z збільшиться за інших однакових обставин на у1 = 1/2 ум. од. і становитиме max Z = 285 +1/2 = 285,5 ум. од. Аналогічно збільшення на одну умовну одиницю третього ресурсу (b3 = 80 + 1 = 81) приведе за інших однакових умов до збільшення цільової функції на у3 = 2 ум. од., що становитиме max Z = = 285 +2 = 287 ум. од. Лише незначні зміни обсягу другого ресурсу ніяк не впливатимуть на значення цільової функції, оскільки у2 = 0.

Додаткові змінні оптимального плану двоїстої задачі відповідають основним змінним прямої задачі і, оскільки останні означають обсяги виробництва кожного виду продукції, відповідні їм у4, у5, у6 та у7 також у певний спосіб мають характеризувати виробництво відповідних видів продукції. За правилами побудови двоїстої задачі очевидно, що додаткові змінні оптимального плану двоїстої задачі показують, наскільки вартість ресурсів перевищує ціну одиниці відповідної продукції. Отже, вони відносно характеризують збитковість виробництва відповідних видів продукції.

Додаткові змінні двоїстої задачі розміщуються в оцінковому рядку останньої симплекс-таблиці у стовпчиках «х1» — «х4». Їх оптимальні значення: у4 = 5; у5 = 5/2; у6 = 0; у7 = 0. Тому витрати на виробництво продукції видів А і В перевищують їх ціну відповідно на 5 та 5/2 ум. од., а для продукції С і D такого перевищення немає. Це підтверджується також попереднім аналізом основних змінних оптимального плану прямої задачі, оскільки за оптимальним планом доцільно виготовляти саме продукцію видів С і D.

Розрахована оптимальна система оцінок забезпечує найменшу загальну вартість усіх ресурсів, що використовуються на підприємстві: min F = 285 ум. од.