- Цветы и растения
- Аквариум и рыбы
- Для работы
- Для сайта
- Для обучения
- Почтовые индексы Украины
- Всяко-разно
- Электронные библиотеки
- Реестры Украины
- Старинные книги о пивоварении
- Словарь старославянских слов
- Все романы Пелевина
- 50 книг для детей
- Стругацкие, сочинения в 33 томах
- Записи Леонардо да Винчи
- Биология поведения человека
Главная  Прочие дисциплины Прочие дисциплины  Книги Книги  Математичне програмування - Наконечний С.І. Математичне програмування - Наконечний С.І. |
Математичне програмування - Наконечний С.І.
3.3.2. Друга теорема двоїстості
Між розв’язками спряжених задач крім рівності значень цільових функцій існує тісніший взаємозв’язок. Для його дослідження розглянемо дві симетричні задачі лінійного програмування.
Пряма задача:

 (3.20)
(3.20)
 .
.
Двоїста задача:

 (3.21)
(3.21)

Для розв’язування задач симплексним методом необхідно звести їх до канонічної форми, для чого в системи обмежень задач (3.20) і (3.21) необхідно ввести відповідно m та n невід’ємних змінних. Поставимо обмеженням кожної задачі у відповідність змінні її двоїстої задачі.

Аналогічно:

Отримали таку відповідність між змінними спряжених задач:

Наступна теорема в літературі, як правило, має назву теореми про доповнюючу нежорсткість.
Теорема (друга теорема двоїстості для симетричних задач). Для того, щоб плани X* та Y* відповідних спряжених задач були оптимальними, необхідно і достатньо, щоб виконувалися умови доповнюючої нежорсткості:
 (3.22)
(3.22)
 . (3.23)
. (3.23)
Доведення. Необхідність. Нехай X* та Y* — оптимальні плани відповідно прямої та двоїстої задач (3.20) i (3.21). З першої теореми двоїстості відомо, що
 ,
,
а також компоненти векторів X* та Y* задовольняють системи обмежень задач (3.20) та (3.21), тобто:
 , (3.24)
, (3.24)
 . (3.25)
. (3.25)
Помножимо (3.24) на  , а (3.25) — на
, а (3.25) — на  і підсумуємо праві та ліві частини. Отримаємо:
і підсумуємо праві та ліві частини. Отримаємо:
 ;
;

Праві частини останніх двох нерівностей не збігаються, але оскільки їх ліві частини однакові, то це означає, що разом вони виконуються лише за умови рівностей, тобто:
 ;
;

Виконаємо перетворення для кожного рівняння:
 ; (3.26)
; (3.26)
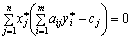 . (3.27)
. (3.27)
Оскільки  , то в рівнянні (3.26) кожна з компонент
, то в рівнянні (3.26) кожна з компонент  , а
, а  , тому виконання рівняння (3.26) можливе лише у тому разі, коли кожний доданок виду
, тому виконання рівняння (3.26) можливе лише у тому разі, коли кожний доданок виду  . Аналогічне міркування проведемо для (3.27), після чого можна висновувати, що
. Аналогічне міркування проведемо для (3.27), після чого можна висновувати, що  . Отже, необхідність умов додаткової нежорсткості доведено.
. Отже, необхідність умов додаткової нежорсткості доведено.
Достатність. За умовою виконуються рівняння
 ,
, 
 ,
,  .
.
Необхідно довести, що X* та Y* — оптимальні плани відповідно прямої (3.20) та двоїстої (3.21) задач.
У кожному рівнянні розкриємо дужки та підсумуємо перше рівняння по  , а друге — по
, а друге — по  . Отримаємо:
. Отримаємо:
 ;
;
 .
.
Ліві частини цих рівнянь однакові, отже, 
 . Тоді за першою теоремою двоїстості, оскільки значення цільових функцій цих задач збігаються, можна висновувати, що X* та Y* — оптимальні плани спряжених симетричних задач. Теорему доведено.
. Тоді за першою теоремою двоїстості, оскільки значення цільових функцій цих задач збігаються, можна висновувати, що X* та Y* — оптимальні плани спряжених симетричних задач. Теорему доведено.
Очевидніший взаємозв’язок між оптимальними планами прямої та двоїстої задач встановлює наслідок другої теореми двоїстості.
Наслідок. Якщо в результаті підстановки оптимального плану однієї із задач (прямої чи двоїстої) в систему обмежень цієї задачі і-те обмеження виконується як строга нерівність, то відповідна і-та компонента оптимального плану спряженої задачі дорівнює нулю.
Якщо і-та компонента оптимального плану однієї із задач додатна, то відповідне і-те обмеження спряженої задачі виконується для оптимального плану як рівняння.
Економічний зміст другої теореми двоїстості стосовно оптимального плану Х* прямої задачі. Якщо для виготовлення всієї продукції в обсязі, що визначається оптимальним планом Х*, витрати одного і-го ресурсу строго менші, ніж його загальний обсяг  , то відповідна оцінка такого ресурсу
, то відповідна оцінка такого ресурсу  (компонента оптимального плану двоїстої задачі) буде дорівнювати нулю, тобто такий ресурс за даних умов для виробництва не є «цінним».
(компонента оптимального плану двоїстої задачі) буде дорівнювати нулю, тобто такий ресурс за даних умов для виробництва не є «цінним».
Якщо ж витрати ресурсу дорівнюють його наявному обсягові  , тобто його використано повністю, то він є «цінним» для виробництва, і його оцінка
, тобто його використано повністю, то він є «цінним» для виробництва, і його оцінка  буде строго більшою від нуля.
буде строго більшою від нуля.
Економічне тлумачення другої теореми двоїстості щодо оптимального плану Y* двоїстої задачі: у разі, коли деяке j-те обмеження виконується як нерівність, тобто всі витрати на виробництво одиниці j-го виду продукції перевищують її ціну сj, виробництво такого виду продукції є недоцільним, і в оптимальному плані прямої задачі обсяг такої продукції  дорівнює нулю.
дорівнює нулю.
Якщо витрати на виробництво j-го виду продукції дорівнюють ціні одиниці продукції  , то її необхідно виготовляти в обсязі, який визначає оптимальний план прямої задачі
, то її необхідно виготовляти в обсязі, який визначає оптимальний план прямої задачі  .
.
Created/Updated: 25.05.2018
 |
|