- Цветы и растения
- Аквариум и рыбы
- Для работы
- Для сайта
- Для обучения
- Почтовые индексы Украины
- Всяко-разно
- Электронные библиотеки
- Реестры Украины
- Старинные книги о пивоварении
- Словарь старославянских слов
- Все романы Пелевина
- 50 книг для детей
- Стругацкие, сочинения в 33 томах
- Записи Леонардо да Винчи
- Биология поведения человека
Главная  Прочие дисциплины Прочие дисциплины  Книги Книги  Математичне програмування - Наконечний С.І. Математичне програмування - Наконечний С.І. |
Математичне програмування - Наконечний С.І.
2.8.3. Оптимальний розв’язок. Критерій оптимальності плану
Симплексний метод уможливлює направлений перебір опорних планів, тобто перехід від одного плану до іншого, який є хоча б не гіршим від попереднього за значенням функціонала. Отже, окремим питанням стає вибір вектора, який необхідно вводити в базис при здійсненні ітераційної процедури симплексного методу.
Розглянемо задачу лінійного програмування (2.36)—(2.38).
Допустимо, що вона має опорні плани і вони є невиродженими. Розглянемо початковий опорний план виду (2.40):

Такому плану відповідає розклад за базисними векторами
 (2.45)
(2.45)
та значення функціонала:
 (2.46)
(2.46)
Кожен з векторів  можна розкласти за векторами базису, причому у єдиний спосіб:
можна розкласти за векторами базису, причому у єдиний спосіб:
 , (2.47)
, (2.47)
тому такому розкладу відповідатиме і єдине значення функціонала:
 . (2.48)
. (2.48)
Позначимо через  коефіцієнт функціонала, що відповідає вектору
коефіцієнт функціонала, що відповідає вектору 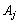 , та
, та  (їх називають оцінками відповідних векторів плану)
(їх називають оцінками відповідних векторів плану)  . Тоді справедливим є таке твердження (умова оптимальності плану задачі лінійного програмування): якщо для деякого плану
. Тоді справедливим є таке твердження (умова оптимальності плану задачі лінійного програмування): якщо для деякого плану  розклад всіх векторів
розклад всіх векторів  у даному базисі задовольняє умову:
у даному базисі задовольняє умову:
 , (2.49)
, (2.49)
то план  є оптимальним розв’язком задачі лінійного програмування (2.36)—(2.38).
є оптимальним розв’язком задачі лінійного програмування (2.36)—(2.38).
Аналогічно формулюється умова оптимальності плану задачі на відшукання мінімального значення функціонала: якщо для деякого плану  розклад всіх векторів
розклад всіх векторів  у даному базисі задовольняє умову
у даному базисі задовольняє умову
 , (2.50)
, (2.50)
то план Х0 є оптимальним розв’язком задачі лінійного програмування.
Отже, для того, щоб план задачі лінійного програмування був оптимальним, необхідно і достатньо, щоб його оцінки  були невід’ємними для задачі на максимум та недодатними для задачі на мінімум.
були невід’ємними для задачі на максимум та недодатними для задачі на мінімум.
Умови оптимальності планів задач лінійного програмування є наслідками двох теорем. Скориставшись введеними в даному параграфі допущеннями та позначеннями, сформулюємо відповідні теореми, а також наведемо їх доведення.
Теорема 2.6. Якщо для деякого вектора  виконується умова
виконується умова  , то план
, то план  не є оптимальним і можна відшукати такий план Х, для якого виконуватиметься нерівність
не є оптимальним і можна відшукати такий план Х, для якого виконуватиметься нерівність  .
.
Доведення. Помножимо (2.47) і (2.48) на  і віднімемо результати відповідно з (2.45) та (2.46). Отримаємо:
і віднімемо результати відповідно з (2.45) та (2.46). Отримаємо:
 ; (2.51)
; (2.51)

 (2.52)
(2.52)
У співвідношенні (2.52) до обох частин додається величина  для
для  . У (2.51)
. У (2.51)  додатні, тому завжди можна знайти таке
додатні, тому завжди можна знайти таке  , що всі коефіцієнти при векторах
, що всі коефіцієнти при векторах  були б невід’ємними, інакше кажучи, отримати новий план задачі виду:
були б невід’ємними, інакше кажучи, отримати новий план задачі виду:
 , якому згідно з (2.52) відповідає таке значення функціонала:
, якому згідно з (2.52) відповідає таке значення функціонала:
 . (2.53)
. (2.53)
Оскільки за умовою теореми  і
і  , то
, то  , що й потрібно було довести.
, що й потрібно було довести.
Якщо розглядається задача на відшукання мінімального значення цільової функції, то формулюється така теорема.
Теорема 2.7. Якщо для деякого вектора  виконується умова
виконується умова  , то план
, то план  не є оптимальним і можна побудувати такий план Х, для якого виконуватиметься нерівність
не є оптимальним і можна побудувати такий план Х, для якого виконуватиметься нерівність  .
.
Доведення аналогічне попередньому.
Created/Updated: 25.05.2018
 |
|