Начало раздела Производственные, любительские Радиолюбительские Авиамодельные, ракетомодельные Полезные, занимательные	Хитрости мастеру Электроника Физика Технологии Изобретения	Тайны космоса Тайны Земли Тайны Океана Хитрости Карта раздела
Использование материалов сайта разрешается при условии ссылки (для сайтов - гиперссылки)

ИЗОБРЕТЕНИЕ
Патент Российской Федерации RU2291546

МАГНИТОВЯЗКИЙ МАЯТНИК

Имя изобретателя: Меньших Олег Фёдорович (RU) 
Имя патентообладателя: Меньших Олег Фёдорович (RU)
Адрес для переписки: 182545, Псковская обл., Невельский р-н, ст. Изоча, Красный Поселок,17, О.Ф. Меньших
Дата начала действия патента: 2005.04.20 

Изобретение относится к физике магнетизма и может быть использовано в качестве устройства преобразования энергии магнитного поля в механическое колебательное движение. Магнитовязкий маятник содержит постоянный магнит и ферромагнитное тело, закрепленное относительно постоянного магнита, например, на скользящей оси для движения с одной степенью свободы в магнитном поле с переменной магнитной индукцией вдоль указанной оси и упруго механически связанное с постоянным магнитом, например, с помощью пружины, закрепленной ее концами соответственно с постоянным магнитом и ферромагнитным телом, причем материал ферромагнитного тела выбран с постоянной времени релаксации магнитной вязкости, соизмеримой, например, с одной десятой периода свободных колебаний ферромагнитного тела, а напряженность поля в зазоре постоянного магнита выбрана предпочтительно насыщающей для ферромагнитного тела. Технический результат: получение механического колебательного движения ферромагнетика, обладающего необходимой магнитной вязкостью и его уменьшающейся относительной магнитной проницаемостью при увеличении напряженности магнитного поля выше некоторого критического уровня.

ОПИСАНИЕ ИЗОБРЕТЕНИЯ

Изобретение относится к физике магнетизма и может быть использовано в качестве устройства преобразования энергии магнитного поля в механическое колебательное движение.

Магнетизм - особая форма взаимодействия электрических токов и магнитов (тел с магнитным моментом) между собой и одних магнитов с другими магнитными материалами. Магнитное взаимодействие пространственно разнесенных тел осуществляется через магнитное поле Н, которое, как и электрическое поле Е, представляет собой проявление электромагнитной формы движения материи. Между магнитными и электрическими полями нет полной симметрии, так как источниками электрических полей являются электрические заряды, а магнитные заряды - монополи пока не обнаружены, хотя теория предсказывает их существование. Источник магнитного поля - движущийся электрический заряд, то есть электрический ток. В атомных масштабах движение электронов и протонов создает орбитальные микротоки, связанные с переносным движением этих частиц в атомах или атомных ядрах, кроме того, наличие у микрочастиц спина обусловливает существование у них спинового магнитного момента. Поскольку электроны, протоны и нейтроны, образующие атомные ядра, атомы, молекулы и все макротела (газы, жидкости, кристаллические и аморфные твердые тела), имеют собственный магнитный момент, то, в принципе, все вещества подвержены влиянию магнитного поля - обладают магнитными свойствами, то есть являются магнетиками. Магнетики подразделяются на диамагнетики, парамагнетики и ферромагнетики. Последние имеют наибольшую магнитную восприимчивость и используются в технике в качестве эффективных магнитов. В них атомные магнитные моменты спонтанно коллинеарно самоориентируются, образуя аномально большие магнитные моменты. У лучших современных магнитных материалов энергетическое произведение (В Н)_max достигает величины 320 Тл·кА/м (40 млн. Гс.э), например у материала с высокой коэрцитивной силой SmCo₃(см., например, Преображенский А.А., Биширд Е.Г. Магнитные материалы и элементы, 3 изд., М., 1986; Февралева И.Е. Магнитотвердые материалы и постоянные магниты, К., 1969; Постоянные магниты, Справочник, М., 1971).

Сложность атомной структуры веществ, построенных из огромного числа микрочастиц, дает практически неисчерпаемое разнообразие их магнитных свойств, связь которых с немагнитными свойствами (электрическими, механическими, оптическими и др.) позволяет использовать исследования магнитных свойств для получения информации о внутренней структуре и других свойствах микрочастиц и макротел. Отметим, что магниты обладают внутренней энергией. В случае однородного магнитного поля в объеме магнита V энергия запасенного магнитного поля W˜ ₀H²V/2, где ₀=1,256·10^-6 гн/м - абсолютная магнитная проницаемость. Причем эта величина энергии практически не расходуется при силовых взаимодействиях с другими магнетиками и сохраняется благодаря постоянному движению заряженных микрочастиц вещества.

Кажущееся противоречие с законом сохранения энергии ставит вопрос об источнике энергии магнитного поля. Таким источником является само вещество магнитов, обладающее запасом магнитной энергии, который за счет процессов, происходящих на микроуровне (атомов и молекул вещества), непрерывно восполняется, а точнее поддерживается на неизменном уровне, если не считать факторов, приводящих к так называемому старению магнитов.

Известный принцип возрастания энтропии и первое и второе начала термодинамики оперируют с теплоэнергетическими преобразованиями, которые всегда (кроме состояния равновесия) идут с затратой энергии при совершении какой-либо работы, большей той, которая составляет саму проделанную работу, а часть затраченной энергии безвозвратно превращается в тепловую. Поэтому к.п.д. всех известных преобразователей энергии всегда меньше единицы. Однако в микромире действует другой процесс: движение микрочастиц обусловлено тепловой энергией - импульс р движения микрочастиц массой m₁определяется как р²/2m₁=(3/2) kT, где k - постоянная Больцмана, Т - температура по шкале Кельвина, а соударения микрочастиц между собой вызывают тепловые процессы - среда нагревается, то есть происходит самовоспроизводящийся обмен энергией, при котором беспредметно говорить о тепловых потерях, поскольку тепловая энергия и является источником движения микрочастиц, а это движение порождает саму тепловую энергию. На поддержание хаотического движения микрочастиц и, следовательно, хаотического распределения магнитных моментов (спинов) в веществе, при котором оно не обнаруживает ощутимых магнитных свойств, затрачивается, по-видимому, больше энергии, чем для тех микрочастиц, которые имеют упорядоченное расположение их магнитных моментов. Поэтому высвободившаяся в результате упорядочения микрочастиц (доменов) часть энергии как раз и составляет энергию магнитного поля. Эта энергия самовосполняемая, определяемая природой процессов превращения энергии на микроуровне.

Однако остается неясным вопрос, каким образом механическая работа, совершаемая действием постоянного магнитного поля на магнитные тела или другие магниты, осуществляется без потери энергии магнитного поля? Ведь факт, что работа магнитных сил не приводит к исчезновению намагниченности постоянных магнитов. Работа совершается действием сил, в частности магнитных сил.

Для ферромагнетиков, подчиняющихся закону Кюри, существует так называемая критическая температура , при которой магнитная восприимчивость становится сравнимой с единицей или даже становится меньшей единицы, и вещество становится из парамагнитного диамагнитным (закон Кюри-Вейсса), то есть магнитная восприимчивость зависит от действия различных факторов - температуры, величины напряженности магнитного поля, механического напряжения и некоторых других.

Одним из интересных свойств ферромагнитных материалов является их так называемая магнитная вязкость магнитное последействие - отставание по времени намагниченности ферромагнетика от изменения напряженности магнитного поля. В наиболее простых случаях изменение намагниченности J в зависимости от времени t описывается формулой

где J₀ и J - соответственно значения намагниченности непосредственно после изменения напряженности Н магнитного поля в момент t=0 и после установления нового равновесного состояния, - константа, характеризующая скорость процесса и называемая постоянной времени релаксации. Значение зависит от природы магнитной вязкости и в различных материалах может изменяться от 10^-9 с до нескольких десятков часов. В общем случае для описания процесса последействия одного значения недостаточно.

Различают два вида магнитной вязкости: диффузионный (рихтеровский) и термо-флуктуационный (иордановский). В первом из них магнитная вязкость определяется диффузией примесных атомов или дефектов кристаллической структуры. Объяснение роли примесей было дано J.Snock, а более строгая теория построена L.Neel и базируется на предположении о преимущественной диффузии примесных атомов в те межатомные промежутки кристалла, которые определенным образом ориентированы относительно направления спонтанной намагниченности. Это создает локальную наведенную анизотропию, приводящую к стабилизации доменной структуры. Поэтому после изменения магнитного поля новая доменная структура устанавливается не сразу, а после диффузного перераспределения примеси, что и является причиной магнитной вязкости. Тепловые флуктуации способствуют преодолению доменными стенками энергетических барьеров в магнитных полях, меньших критического поля. В высококоэрцитивных сплавах, состоящих из однодоменных областей, наблюдается особенно большая магнитная вязкость, так как в этом случае термические флуктуации сообщают дополнительную энергию для необратимого вращения спонтанной намагниченности тех частиц, потенциальная энергия которых во внешнем магнитном поле недостаточна для их перемагничивания. Кроме этих основных механизмов магнитной вязкости существуют и другие. Например, в некоторых ферритах вклад магнитной вязкости дает перераспределение электронной плотности (диффузия электронов между ионами разной валентности). С магнитной вязкостью тесно связаны такие явления в ферромагнетиках, как потери на перемагничивание, временной спад относительной магнитной проницаемости (и ее частотная зависимость (см., например, Kronmuller H., Nachwirkung in Ferromsgnetika, 1068; С. В.Вонсовский, Магнетизм, М., 1971; Д.Д.Мишин, Магнитные материалы, М., 1981).

Известные свойства магнитной вязкости ферромагнетиков лежат в основе заявляемого технического решения. Кроме самих этих известных свойств, не имеется в настоящее время каких-либо аналогов (прототипов) заявляемому предложению, поэтому формула изобретения не содержит ограничительной части.

Целью изобретения является получение механического колебательного движения ферромагнетика, обладающего необходимой магнитной вязкостью и его уменьшающейся относительной магнитной проницаемостью при увеличении напряженности магнитного поля выше некоторого критического уровня.

Указанная цель достигается в устройстве - магнитовязком маятнике, содержащем постоянный магнит и ферромагнитное тело, закрепленное относительно постоянного магнита, например, на скользящей оси для движения с одной степенью свободы в магнитном поле с переменной магнитной индукцией вдоль указанной оси и упруго механически связанное с постоянным магнитом, например, с помощью пружины, закрепленной ее концами соответственно с постоянным магнитом и ферромагнитным телом, причем материал ферромагнитного тела выбран с постоянной времени релаксации магнитной вязкости, соизмеримой, например, с одной десятой периода свободных колебаний ферромагнитного тела, а напряженность поля в зазоре постоянного магнита выбрана предпочтительно насыщающей для ферромагнитного тела.

Достижение поставленной цели в заявляемом техническом решении объясняется непрерывной энергетической подкачкой упругих, в принципе затухающих, колебаний со стороны магнитного поля постоянного магнита с переменной магнитной индукцией вдоль оси колебательного движения ферромагнитного тела, которое обладает свойством магнитной вязкости и уменьшением своей относительной магнитной проницаемости при увеличении напряженности магнитного поля, превышающего некоторый пороговый уровень, причем явление резонанса колебаний ферромагнитного тела наступает при выборе постоянной релаксации у материала ферромагнитного тела, соизмеримой с периодом собственных колебаний пружинного маятника с заданными массой ферромагнитного тела и жесткостью пружины. При прохождении ферромагнитного тела в магнитном поле, напряженность которого в данной области соответствует порогу магнитного насыщения для выбранного ферромагнитного материала, происходит экспоненциальный спад намагниченности ферромагнитного тела, что ослабляет силовое торможение магнитным полем ферромагнитного тела и способствует увеличению его амплитуды колебаний, а при нахождении ферромагнитного тела в зонах сниженной напряженности магнитного поля (вблизи амплитудных значений текущей координаты центра инерции ферромагнитного тела), наоборот, его относительная магнитная проницаемость экспоненциально возрастает, что приводит при обратном такте движения ферромагнитного тела в направлении градиента магнитного поля к дополнительному увеличению силы, приложенной к ферромагнитному телу, со стороны магнитного поля. При этом важным условием для обеспечения резонансных колебаний ферромагнитного тела (то есть условий достижения максимума амплитуды колебаний) является выбор постоянной релаксации материала ферромагнитного тела, величина которой должна быть соизмерима с периодом Т собственных колебаний пружинного маятника ˜Т=(1/2 )(m/k)^1/2, где m - масса ферромагнитного тела (с учетом других присоединенных масс), k - жесткость пружины. Соблюдение этого условия создает возможность синфазной силовой «подкачки» колебаний ферромагнитного тела в составе пружинного маятника.

Заявляемое техническое решение понятно из представленного на чертежах схемного и графического материала.

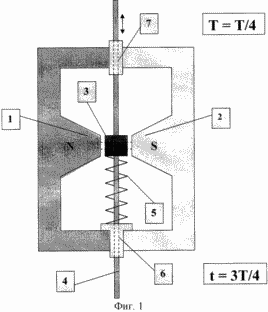На фиг.1 представлен схематический вид конструктивного исполнения магнито-вязкого маятника, содержащего постоянный магнит с северным 1 и южным 2 полюсами, ферромагнитное тело 3, закрепленное на скользящей оси 4 и связанное с пружиной 5, другой конец которой закреплен относительно постоянного магнита, а скользящая вдоль одного направления ось 4 свободно связана с направляющими втулками 6 и 7, закрепленными в постоянном магните, являющемся корпусом устройства.

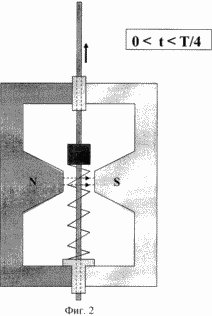
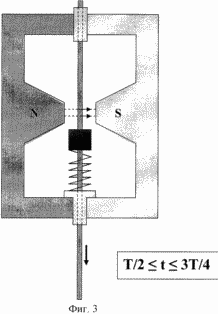
На фиг.2 и 3 представлены различные состояния колебательного движения ферромагнитного тела в различные моменты времени - в различных фазах его колебаний.

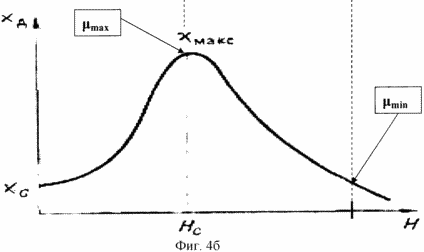
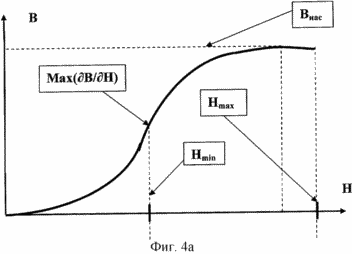	На фиг.4а и 4б представлены соответственно графики зависимости магнитной индукции В от напряженности Н магнитного поля, действующего на ферромагнитное тело, и зависимость его относительной магнитной проницаемости (магнитной восприимчивости =-1) от действующего в ферромагнитном веществе значения напряженности Н магнитного поля без учета магнитной вязкости (кривая Столетова).
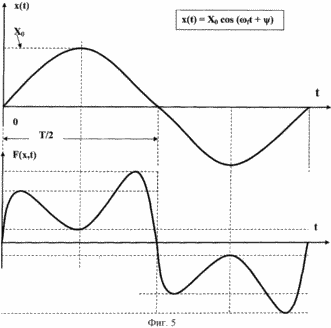	На фиг.5 представлены эпюры механического колебания ферромагнитного тела (его центра инерции как материальной точки) вдоль выбранного направления колебаний, обозначенного как ось х (ось ординат), в функции времени t (ось абсцисс), а и действия синфазной силовой «подкачки» колебательного движения со стороны магнитного поля постоянного магнита на ферромагнитное тело с его изменяющейся во времени (с частотой колебаний) относительной магнитной проницаемостью (t) за счет эффектов магнитной вязкости и указанной выше зависимости (Н), при которой (Н)/( Н)·(dH/d|x|)<0.

ПРИНЦИП ДЕЙСТВИЯ ЗАЯВЛЯЕМОГО УСТРОЙСТВА

Будем полагать, что ферромагнитное тело 3 со скользящей осью 4 (фиг.1) массой m с центром тяжести, имеющим координату x₀=0 в равновесном невозмущенном состоянии, как изображено на фиг.1, где координатная ось х совпадает со скользящей осью 4 устройства, и вдоль этой координаты осуществляется движение материальной точки (центра тяжести ферромагнитного тела 3 вместе со скользящей осью 4) с одной степенью свободы, совершает колебательное движение с участием действующих сил со стороны пружины 5 и магнитного поля постоянного магнита, образованного между его полюсами 1 и 2, поле между которыми имеет напряженность Н_max, достаточную для магнитного насыщения ферромагнитного вещества, используемого в устройстве. В этом поле в установившемся режиме (то есть за промежуток времени порядка 2,2 от момента включения магнитного поля) относительная магнитная проницаемость ферромагнитного вещества падает до величины _min, как указано на фиг.4б. При этом в магнитном поле напряженностью Н_min это ферромагнитное вещество имеет =_max, как это следует из графиков фиг.4.

Как известно, если на материальную точку массы m действует центральная сила, пропорциональная отклонению точки (линейная сила) F=- kx при k=const, что имеет место в случае пружинного маятника, частота колебаний с одной степенью свободы (вдоль оси х) равна ₀=(k/m)^1/2. Полагая силу трения пропорциональной скорости движения материальной точки dx/dt, уравнение движения записывается в виде:

где F(x,t) - сила, действующая на рассматриваемое ферромагнитное тело как материальную точку со стороны магнитного поля, являющаяся функцией координаты точки относительно ее устойчивого положения равновесия в центре между полюсами 1 и 2 постоянного магнита и рассматриваемая для колебательного процесса в пружинном маятнике в качестве внешней вынуждающей силы.

При F(x,t)=0 из (2) следует, что колебания в пружинном маятнике являются свободными и затухающими. В одном из частных решений дифференциального уравнения для свободных затухающих колебаний (а не апериодического процесса) интегрирование дает для а²<4km следующее выражения для движения:

где 2m/a - постоянная времени затухающего колебания в системе, и колебания в ней происходят с частотой _f, равной

с декрементом затухания

где Т - период колебания.

При вынужденных колебаниях с внешней силой F(x,t)0, если вынуждающую силу принять изменяющейся по гармоническому закону, уравнение (2) имеет вид:

с частным решением

x(t)=Х₀ cos ( t-), где

где ₀=(k/m)^1/2 - собственная частота свободных незатухающих колебаний точки.

При этом х ₀( ) представляет (амплитудную) резонансную кривую колеблющейся точки с максимумом при

Чтобы возникшие, например, с помощью определенного воздействия (толчка) на пружинный маятник колебания непрерывно поддерживались на постоянном уровне амплитуды, необходимо подействовать на такую механическую систему внешней периодической силой, компенсирующей потери, чтобы декремент затухания в колеблющейся системе был равен нулю, то есть =a·/ _fm=0. Отметим сразу, что если эти внешние силы будут превышать необходимую величину, то это приведет лишь к увеличению амплитуды колебаний, которые и в этом случае будут незатухающими. и отметим, что рассмотрение чисто гармонической внешней силы в уравнении (6) принято лишь для упрощения рассмотрения принципа действия заявляемого технического решения, но и возможно действие периодически повторяющихся силовых воздействий, представляющих собой сложное по спектру внешнее колебание, которое может быть разложено в ряд Фурье, и в этом случае возможно решение задачи путем сопоставления частных решений с отдельными спектральными составляющими такого внешнего колебания.

Без разложения F(x,t) в ряд Фурье получают решение в форме

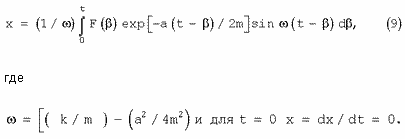
В частности, внешняя вынуждающая периодическая сила F(x,t) может носить импульсный характер. Важно лишь, чтобы эти воздействия, во-первых, восполняли энергетические потери при колебании ( =0), во-вторых, носили периодический (с частотой колебаний пружинного маятника) характер и, в-третьих, были соответственно сфазированы с положениями движущегося ферромагнитного тела, что поясняется на фиг.5.

Проанализируем, как выполняются эти требования в данном устройстве.

Поскольку сила F(x,t) возникает именно вследствие взаимодействия ферромагнитного тела 3 с магнитным полем постоянного магнита и это тело совершает колебательное движение в поле магнитных полюсов 1 и 2 и вне их (то есть в значительно ослабленном магнитном поле), то и сами силы, возникающие при этом движении, носят строго периодический характер. Так что это требование (периодичности) соблюдается автоматически, как в генераторе с колебательным контуром в режиме самовозбуждения.

Второй член дифференциального уравнения (6) представляет собой в физическом смысле силу трения, то есть определяет потери энергии при колебательном движении (в данном случае потери на трение скользящей оси 4 в направляющих втулках 6 и 7, учет возможной присоединенной нагрузки и т.д.), поэтому требование =0 означает, что энергия потерь за каждый период колебаний, определяемая декрементом затухания, должна компенсироваться энергией р²/2m с разностным импульсом р внешней силы в каждом из полупериодов колебания, равным

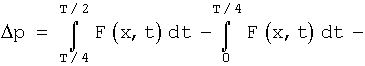
разностный средний импульс внешней силы магнитного поля за половину периода колебания, поскольку такие импульсивные действия возникают дважды за период Т, когда ферромагнитное тело выходит из магнитного зазора вверх и затем возвращается в него, двигаясь вниз, как это видно из фиг.2, после чего двигается вниз и вновь возвращается, как это видно на фиг.3. Соответствующие временные фазы колебания указаны на этих чертежах (фиг.1-3). Иначе говоря, должно соблюдаться условие «баланса амплитуд», которое несложным преобразованием с учетом усреднения скорости колеблющейся точки за период с заданной амплитудой колебаний X₀ находится в неявном виде из выражения:

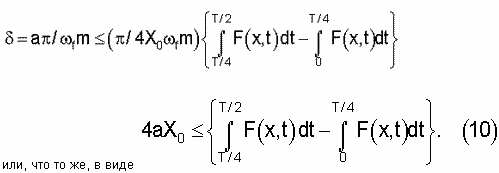
Декремент затухания механической системы определяется опытным путем в каждом конкретном исполнении устройства в отсутствие магнитного поля, масса ферромагнитного тела с другими присоединенными к нему массами и частота колебаний маятника и легко определимы. Поэтому второе из условий осуществления устройства (о балансе амплитуд) выполняется согласно (10) заданием соответствующих требований к свойствам ферромагнитного вещества и магнитному полю постоянного магнита.

Из рассмотрения (10) видно, что интегралы определяет разностный средний импульс силы. Следовательно, эти интегралы задают среднюю силу действия магнитного поля на ферромагнитное тело за время Т/2, в течение которого ферромагнитное тело из своего устойчивого положения равновесия движется вверх до амплитудного значения х=Хо и затем возвращается в исходное положение в центре магнитного зазора постоянного магнита. Эта сила равна:

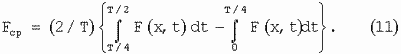
В том случае, если ферромагнитное вещество не изменяет своих магнитных свойств, то есть не учитывая свойства магнитной вязкости и уменьшения относительной магнитной проницаемости при увеличении напряженности магнитного поля, конечно, никакого поддержания колебательного процесса в устройстве не происходило бы, поскольку векторы сил от действия магнитной системы, приложенные к ферромагнитному веществу, всегда направлены в сторону центра тяготения магнитной системы, то есть к координате х=0, и за первую четверть периода ферромагнитное тело, движущееся от положения равновесия к своему амплитудному значению, преодолевает эту силу тяготения, теряя дополнительно (кроме действия самой пружины!) свою кинетическую энергию, а за вторую четверть периода получает обратно эту же порцию энергии, поэтому F_cp=0, так как значения мгновенных сил для любой из координат в промежутке 0x Х₀ как при движении ферромагнитного тела от центра, так и к центру, равны между собой.

Иначе дело обстоит в случае специального выбора материала для ферромагнитного тела в данном устройстве. Обратившись к фиг.4б, можно отметить, что изменение относительной магнитной проницаемости ферромагнитного вещества на ниспадающей кривой (Н) с учетом действия магнитной вязкости приводит в динамике взаимодействия ферромагнитного тела с магнитным полем, локализованным между полюсами 1 и 2 постоянного магнита, к различию сил тяготения ферромагнитного тела к центру притяжения магнитной системы в одних и тех же координатных точках интервала 0х Х₀. Действительно, когда ферромагнитное тело под действием пружины проходит мимо полюсов магнита, оно снижает свою магнитную восприимчивость из-за насыщения ферромагнитного вещества в сильном магнитном поле, и ему легче покинуть магнитную систему, чем в случае, если бы такого снижения магнитной восприимчивости не происходило бы. С другой стороны, когда тело возвращается из своего амплитудного положения к центру магнитного притяжения, оно успевает восстановить величину своей магнитной проницаемости, то есть увеличивает свою магнитную восприимчивость, в связи с чем обладает большим, чем в первом случае, магнитным моментом и сильнее притягивается на тех же координатных точках к магнитной системе, что вызывает дополнительное ускорение такого движения. Из этого следует, что F_cp>0. Точно такая же картина будет наблюдаться и во второй половине периода колебания, когда ферромагнитное тело устремится по инерции сверху вниз, сжимая пружину превращением своей кинетической энергии во внутреннюю энергию сжимаемой пружины. В этом и состоит физический механизм энергетической подкачки колеблющейся системы за счет свойства применяемого ферромагнетика, изменяющего свою магнитную восприимчивость в неоднородном магнитном поле. При этом важно иметь такую величину магнитной вязкости ферромагнетика, которая согласовывалась бы с динамикой колебательного движения ферромагнитного тела. Это приводит к формулированию последнего необходимого и достаточного условия поддержания в системе незатухающих колебаний - условию «баланса фаз», которое состоит в синфазировании силовых импульсов от действия магнитной системы на ферромагнитное тело при его движении. Это означает, что эти силовые «добавки» со стороны магнитного поля должны возникать на этапе приближения ферромагнитного тела к центру тяготения магнитной системы и, наоборот, магнитная система должна ослаблять свое силовое влияние на ферромагнитное тело, движущееся от центра тяготения. Эти процессы, так же как и периодичность действия сил магнитного поля на ферромагнитное тело, осуществляются автоматически, и вопрос состоит лишь в их эффективности. Для анализа этого вопроса и необходимо рассмотрение динамики проявления магнитной вязкости, характеризуемой одним параметром - постоянной времени релаксации, как это следует из выражения (1). Качественное разрешение вопроса состоит в рассмотрении разных вариантов поведения магнитной вязкости в рассматриваемом устройстве. Так, если постоянная времени существенно меньше периода механических колебаний пружинного маятника /Т<1, то ферромагнитное вещество будет очень быстро восстанавливать значение своей магнитной проницаемости при изменении магнитного поля, связанного с движением в нем ферромагнитного тела, и различие сил в одних и тех же координатных точках траектории движения тела от центра притяжения и к нему будет незначительным или его практически не будет вовсе, и поэтому необходимой подкачки колеблющаяся система получать не будет, и колебания в ней затухнут. С другой стороны, если постоянная релаксации будет во много раз больше периода колебаний /Т>1, то это будет означать практическую неспособность ферромагнетика как-либо заметно изменять свою магнитную восприимчивость в изменяющемся по напряженности магнитном поле при заданной частоте колебаний, поэтому и колебания в системе станут затухающими. Так что для обеспечения требуемой энергетической подкачки необходимо, чтобы величина постоянной релаксации была жестко согласована с периодом колеблющейся механической системы, то есть возникают требования к минимальной и максимальной границам величин постоянной релаксации, в пределах которых возможно обеспечение незатухающих механических колебаний в рассматриваемой системе, то есть _min< <_max.

Таким образом, система проявляет пороговые свойства по отношению к выбору ферромагнетиков в требуемом диапазоне постоянных релаксации. Качественно рассматривая границы диапазона по , можно указать, что минимальная граница _min определяется временем эффективного взаимодействия ферромагнитного тела с магнитной системой, то есть временем пробега длины полюсов 1 и 2 постоянного магнита, как это видно из фиг.1. Пусть длина (по оси х) составляет величину Х₀ (часть от амплитуды колебаний). Тогда при частоте колебаний _f (см. выражение (4)) с учетом переменной скорости колеблющейся материальной точки - центра тяжести ферромагнитного тела - вдоль оси х по гармоническому закону получим время пролета этой точки внутри магнитной системы t₁=g₁( , Х₀, ). В явном виде этот интервал времени находится интегрированием и составляет величину t₁=(Т/2 ) arcsin . Учитывая время установления в экспоненциальном процессе как t_уст=2,2 , приходим к установлению границы _min=t₁/2,2=(0,45/ _f) arcsin .

Очевидно, что по тем же соображениям максимальная граница по определяется временем пребывания ферромагнитного тела в промежутке 2(1- )Х₀, и это время t₂=g₂(, Х₀, ) и равно t₂=2[(Т/4)- t₁]=(-2 arcsin )/_f и тогда получим для _max=(-2 arcsin )/2,2_f. В результате такого анализа получаем важные для определения конструкции устройства сведения из анализа отношения найденных выше граничных значений постоянных релаксации

Поскольку необходимо выполнить требование _max/ _min1, то из этого вытекает ограничение на величину относительной длины магнитных полюсов системы (в сравнении с амплитудой колебаний), так что arcsin (/2) и, следовательно, величина должна быть =L/X₀1, где L - длина полюсов 1 и 2 вдоль оси x. Из полученного условия можно сделать вывод, что амплитуда колебаний и длина полюсов магнита в предельном случае могут быть и одинаковыми, и при этом центр тяжести ферромагнитного тела в крайних своих положениях (фиг.2 и 3) выходит за пределы краев магнитных полюсов на половину их длины. При меньших значениях - еще гораздо дальше.

Следует заметить, что подбор ферромагнетика с нужным значением может оказаться затруднительным, так как ассортимент такого рода веществ с требуемыми параметрами по магнитной вязкости и крутизне падающей части характеристики /H не столь уж богат. Поэтому следует подобрать ферромагнетик с близкими к требуемым параметрами, а затем легко подстроить под них варьируемые в эксперименте параметры механической системы - массу ферромагнитного тела, жесткость пружины, величину магнитного поля, длину магнитных полюсов и даже пространственное положение устройства (в последнем случае изменяется составляющая силы тяготения массы ферромагнитного тела в гравитационном поле, спроектированная на ось х), чтобы соответствующим образом изменить период колебаний Т.

Выше была рассмотрена динамика работы системы в предположении линейности центральной силы, действующей на материальную точку (центр инерции движущегося объекта - ферромагнитного тела и скользящей оси), от величины смещения х, и при этом условно предполагалось, что действие магнитного поля как упругой среды соотнесено к свойствам пружины с какой-то другой ее жесткостью, большей, чем собственная жесткость пружины. Однако, строго говоря, это не так, поскольку сила взаимодействия магнитного поля с ферромагнитным телом, обладающим магнитным моментом M(x,t) как функции координат и времени с учетом динамики движения его вдоль координаты х, не является линейной функцией смещения ферромагнитного тела вдоль заданного направления, а и является функцией времени с учетом временного характера изменения относительной магнитной проницаемости из-за свойства магнитной вязкости, то есть =f(x, t) при заданной частоте _fколебаний. Следовательно, третий член левой части уравнения (6) вместо члена kx должен содержать иное, более сложное выражение, что, в свою очередь, повлияет на результат решения этого уравнения, в частности на значение периода колебаний магнитовязкого маятника. Расчет такого рода сложен и требует привлечения соответствующего математического анализа, однако не изменит качественно тех положений, которые лежат в основе объяснения возможности поддержания непрерывно во времени колебательного движения ферромагнитного тела.

Интересно и отметить, что из условия (10) видно, что амплитуда колебаний Х₀связана со средним значением разностного импульса силы подкачки и величиной вносимого в систему механического трения. Ясно, что для увеличения амплитуды колебаний, то есть для увеличения механической энергии колебательного движения W=m_f ²X₀ ²/4 следует уменьшать трение в колеблющейся механической системе, то есть уменьшать коэффициент а. В рассматриваемой схеме (фиг.1) это касается, главным образом, уменьшения коэффициента трения скользящей оси 4 в направляющих втулках 6 и 7. Кроме того, трение (потери) возникает и в самой пружине.

Поэтому для снижения этих потерь можно скользящую ось «закрепить» на магнитных подушках по ее концам и совсем устранить из схемы пружину, поскольку сама магнитная система обладает необходимыми упругими свойствами (правда, нелинейно зависящими от величины смещения по координате х, что только скажется на составлении и решении соответствующего дифференциального уравнения движения). При отсутствии пружины 5 ось 4 может быть выполнена неподвижно закрепленной в теле постоянного магнита, а ферромагнитное тело 3 будет при этом скользить вдоль этой оси при своем колебательном движении, и в этом случае необходимо, по возможности, снизить коэффициент трения скольжения этого тела относительно оси. Допустимы и другие модификации конструктивного исполнения заявляемого технического решения, в основе действия которых используются свойства магнитной вязкости и падения магнитной восприимчивости ферромагнетика с увеличением напряженности магнитного поля.

Общая постановка задачи о нахождении мгновенных сил F(x,t) при движении ферромагнитного тела массы m с амплитудой и частотой колебаний соответственно X₀и _f, с учетом заданного однородного магнитного поля Н_мах между магнитными полюсами с их относительной длиной сводится к интегрированию дифференциалов сил, приложенных к дифференциальным объемам ферромагнитного тела (разбиваемого сечениями S, ортогональными оси х, на дифференциальные объемы dv=S dx), вдоль направления от х=0 до х=Х₀, а затем к аналогичному интегрированию, но уже по обратному пути - от х=X₀до х=0. При этом необходимо учитывать динамику установления в рассматриваемых дифференциальных объемах ферромагнитного тела магнитной восприимчивости как функции текущего значения напряженности поля Н(х), временной процесс установления (t) и мгновенную скорость движения данного дифференциального объема, которая в связи с нелинейным действием упругости магнитного поля изменит гармонический характер движения в целом ферромагнитного тела.

При этом центром тяготения магнитной системы в случае однородности поля между полюсами 1 и 2 (фиг.1) постоянного магнита следует принимать сечение при х=0, то есть на середине между полюсами. Для каждого из рассматриваемых дифференциальных объемов следует вычислить их текущий (меняющийся во времени при перемещении по х-координате) дифференциальный магнитный момент dM(x,t)=J(x,t)dv=SJ(x,t)dx с учетом выражения (1), после чего определяется соответствующая дифференциальная сила тяготения данного дифференциального объема ферромагнитного тела, находящегося на координате х в магнитном поле с градиентом Н/Х в данной координатной точке из выражения:

где J(x,t) - мгновенное (зависящее от координаты) значение намагниченности данного дифференциального объема ферромагнитного тела, учитывающее выражение (1).

После вычисления указанных выше двух интегралов окажется, что первый из них больше второго на величину TF_cp/2>0, как это видно из формулы (11), выражающей усредненную силу подкачки колеблющейся системы, которая должна быть больше усредненной силы трения в механической системе, учитывающей все возможные потери энергии в ней.

Наличие F_cp>0 означает, что в систему с потерями вводится «отрицательное сопротивление», действие которого поддерживает колебательное состояние в системе на определенной амплитуде колебаний, учитывая нелинейные свойства упругости магнитного поля по отношению к ферромагнитному телу и то, что потери на трение считаются линейно связанными с этой амплитудой, то есть уменьшаются при снижении амплитуды. В общем случае незатухающие колебания в системе будут иметь место при выполнении условия, аналогичного условию (10).

Наконец, следует отметить, что механическая энергия колебательного движения рассматриваемого пружинного (или иного) маятника W=m_f ² X₀ ²/4 не является той энергией, которая «извлекается» из взаимодействия ферромагнитного тела с магнитным полем. Полезная получаемая от такого взаимодействия энергия равна той доле от общей кинетической энергии W, которая лишь восполняет потери в механической системе, определяемые ее декрементом затухания, то есть составляет лишь небольшую часть W˜ W. Однако, несмотря на относительную малость этой энергии, принципиально важно то, что она черпается из энергии магнитного поля постоянного магнита и работы микрочастиц, определяющих свойства ферромагнетика.

Из полученных данных следует, что для практической реализации предлагаемого магнитовязкого маятника необходимо иметь дело с ферромагнетиками с достаточно высокой инерционностью установления относительной магнитной проницаемости при изменении напряженности магнитного поля. Так, для маятника с частотой колебаний 5 Гц необходимо подобрать ферромагнетик с порядка 17 мс, если выбрать =0,707. При этом и необходимо обеспечить условие, что ( (H)/H)(dH/dx)<0.

Однако, несмотря на эти сложности выбора подходящего ферромагнетика, чрезвычайно интересно как с практической, так и с научной точек зрения построение такого устройства, в котором «работают» микрочастицы вещества ферромагнетика, определяющие его магнитную вязкость, совместно с изменяющимся во времени магнитным полем постоянного магнита для движущегося возвратно-поступательно ферромагнетика. Это колебательное движение задается пружинным механическим маятником, поддерживается в форме незатухающих колебаний за счет работы микрочастиц вещества, а энергетическим источником такой силовой подкачки выступает магнитное поле постоянного магнита, то есть без применения каких-либо внешних источников энергии. Совершенно ясно, что для обеспечения условия баланса амплитуд достаточно при выполнении всех необходимых условий фазового синхронизма и выбора подходящего материала ферромагнетика просто выбрать нужную индукцию магнитного поля.

Заявляемое техническое решение является принципиально новым, не имеющим аналогов в мировом приборостроении. Оно особенно интересно тем, что позволяет надеяться, что скрытая в постоянных магнитах и ферромагнитном веществе энергия может быть извлечена для решения различных энергетических проблем.

Демонстрация действия заявляемого технического решения без подключенных к нему внешних источников энергии заставит ученых-физиков переосмыслить некоторые представления о физике магнетизма и других закономерностях, которые предстоит открыть для реализации извечной мечты человека - энергетического изобилия.

Заявляемое техническое решение может быть практически осуществлено уже в настоящее время в тех организациях, которые занимаются исследованием ферромагнитных веществ и их физикой, например в Физическом институте РАН (г.Москва).

ДОПОЛНЕНИЕ К ЗАЯВКЕ «МАГНИТОВЯЗКИЙ МАЯТНИК»

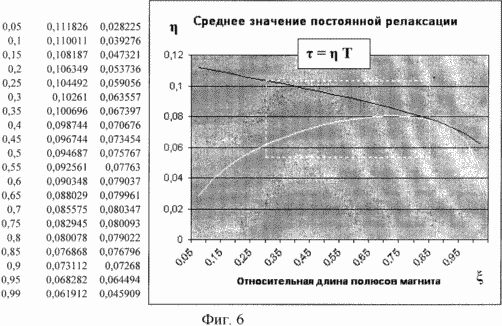
Анализ величины постоянной релаксации магнитной вязкости на основе усреднения граничных значений этой величины как функции относительной длины полюсов постоянного магнита вдоль оси х колебательного движения ферромагнитного тела (фиг.1) методом вычисления среднего арифметического значения граничных величин (светлая кривая) и среднего геометрического этих величин _minи _max (темная кривая на графике) показал, что предпочтительные значения величины в области практических величин находятся в диапазоне значений 0,05<<0,11. Поэтому автор в формуле изобретения указал, что величина постоянной времени релаксации магнитной вязкости выбираемого ферромагнитного вещества «соизмерима, например, с одной десятой периода свободных колебаний ферромагнитного тела», хотя конкретное значение этой величины имеет указанный разброс и уточняется экспериментально, например изменением периода колебаний ферромагнитного тела для выбранного ферромагнитного материала выбором параметра k жесткости пружины или уточнением величины присоединенной массы ферромагнитного тела. Приведенный в заявке пример для =0,707 соответствует экстремальному средне-арифметическому значению =0,08518 Т (то есть соответствует ˜Т/12).

Соответствующие данные вычислений средней арифметической и средней геометрической величин () приведены в таблице и на графике (см. фиг.6). Пунктирным прямоугольником на графике показана предпочтительная область выбираемых величин.

ФОРМУЛА ИЗОБРЕТЕНИЯ

Магнитовязкий маятник, содержащий постоянный магнит и ферромагнитное тело, закрепленное относительно постоянного магнита, например, на скользящей оси для движения с одной степенью свободы в магнитном поле с переменной магнитной индукцией вдоль указанной оси и упруго-механически связанное с постоянным магнитом, например, с помощью пружины, закрепленной ее концами соответственно с постоянным магнитом и ферромагнитным телом, причем материал ферромагнитного тела выбран с постоянной времени релаксации магнитной вязкости, соизмеримой, например, с одной десятой периода свободных колебаний ферромагнитного тела, а напряженность поля в зазоре постоянного магнита выбрана предпочтительно насыщающей для ферромагнитного тела.

Версия для печати
Дата публикации 16.02.2007гг

НОВЫЕ СТАТЬИ И ПУБЛИКАЦИИ
	Технология изготовления универсальных муфт для бесварочного, безрезьбового, бесфлянцевого соединения отрезков труб в трубопроводах высокого давления (имеется видео)
	Технология очистки нефти и нефтепродуктов
	О возможности перемещения замкнутой механической системы за счёт внутренних сил
	Свечение жидкости в тонких диэлектрических каналох
	Взаимосвязь между квантовой и классической механикой
	Миллиметровые волны в медицине. Новый взгляд. ММВ терапия
	Магнитный двигатель
	Источник тепла на базе нососных агрегатов